Question

已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的焦距为2，且与直线y=x-

3

相切．
（1）求椭圆C的方程；
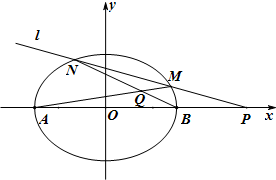
（2）设椭圆C的左、右顶点分别为A，B，过点P（3，0）的直线l与椭圆C交于两点M，N（M在N的右侧），直线AM，BN相交于点Q，求证：点Q在一条定直线上．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（1）由椭圆的焦距为2得到a和b的关系，再由直线与椭圆相切，联立方程组后由判别式等于0得到关于a的方程，从而求得a²的值，则b²可求，椭圆的方程可求；
（2）设出直线l的方程，和椭圆方程联立后化为关于x的一元二次方程，利用根与系数关系求得M，N两点的横坐标的和与积，用M，N的坐标表示出直线AM和BN的方程，两直线方程联立后消去y，结合前面的根与系数关系整体运算求得x值为定值，从而证明点Q在一条定直线上．

解答： （1）解：∵椭圆的焦距为2，
∴b²=a²-1且a²＞1，
于是椭圆方程为（a²-1）x²+a²y²-a²（a²-1）=0．
将y=x-

3

代入得(2a2-1)x2-2

3

a2x+4a2-a4=0．
∵直线与椭圆相切，
∴△=(-2

3

a2)2-4(2a2-1)(4a2-a4)=0．
即a⁴-3a²+2=0．
∵a²＞1，
∴a²=2，则b²=1．
故所求椭圆方程为

x2

2

+y2=1；                                           
（2）证明：由题意可设直线l的方程为y=k（x-3），
联立方程

y=k(x-3) x2 2 +y2=1

，得（2k²+1）x²-12k²x+2（9k²-1）=0．
∵直线l与椭圆C交于M（x₁，y₁），N（x₂，y₂）两点，
∴△=144k⁴-8（2k²+1）（9k²-1）＞0⇒k2＜

1

7

，
由韦达定理得x1+x2=

12k2

2k2+1

，x1x2=

2(9k2-1)

2k2+1

，
则(x2-x1)2=(x1+x2)2-4x1x2
=

144k4

(2k2+1)2

-

8(9k2-1)

2k2+1

=

8-56k2

(2k2+1)2

．
又M在N的右侧，
∴x2-x1=-

2 2

1+2k2

1-7k2

，
∵A(-

2

，0)，B(

2

，0)，
∴lAM：y=

y1

x1+ 2

(x+

2

)，lAN：y=

y2

x2- 2

(x-

2

)．
设直线AM、BN相交于点Q（x，y），
由上面两直线方程消去y得：

x+ 2

x- 2

=

y2

y1

•

x1+ 2

x2- 2

⇒

x+ 2

x- 2

=

k(x2-3)(x1+ 2 )

k(x1-3)(x2- 2 )

=

x1x2-3x1+ 2 x2-3 2

x1x2-3x2- 2 x1+3 2

⇒

x

2

=

2x1x2-3(x1+x2)+ 2 (x2-x1)

2 (x1+x2)-6 2 +3(x2-x1)

=

4(9k2-1) 2k2+1 - 36k2 2k2+1 - 4 1-7k2 2k2+1

12 2 2k2+1 -6 2 - 6 2 1-7k2 2k2+1

⇒

x

2

=

-4-4 1-7k2

-6 2 -6 2 1-7k2

=

2

3

⇒x=

2

3

．
故点Q在定直线x=

2

3

上．

点评：本题主要考查椭圆方程的求法，考查了直线与椭圆的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系求解是处理这类问题的最为常用的方法，但圆锥曲线的特点是计算量比较大，要求考试具备较强的运算推理的能力，是高考试卷中的压轴题．