题目内容
设数列{an}共有n(n≥3,n∈N)项,且a1=an=1,对每个i(1≤i≤n-1,i∈N),均有
∈{
,1,2}.
(1)当n=3时,写出满足条件的所有数列{an}(不必写出过程);
(2)当n=8时,求满足条件的数列{an}的个数.
| ai+1 |
| ai |
| 1 |
| 2 |
(1)当n=3时,写出满足条件的所有数列{an}(不必写出过程);
(2)当n=8时,求满足条件的数列{an}的个数.
考点:数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(1)利用新定义,可得a2=
或a2=1或a2=2,即可得出结论;
(2)确定由符合上述条件的7项数列{bn}可唯一确定一个符合条件的8项数列{an},bi (1≤i≤7)中有k个2;从而有k个
,7-2k个1.当k给定时,{bn}的取法有
种,易得k的可能值只有0,1,2,3,即可得出结论.
| 1 |
| 2 |
(2)确定由符合上述条件的7项数列{bn}可唯一确定一个符合条件的8项数列{an},bi (1≤i≤7)中有k个2;从而有k个
| 1 |
| 2 |
| C | k 7 |
| C | k 7-k |
解答:
解:(1)当n=3时,a1=a3=1.
因为
∈{
, 1 , 2 },
∈{
, 1 , 2 },
即a2∈{
, 1 , 2 },
∈{
, 1 , 2 },
所以a2=
或a2=1或a2=2.
故此时满足条件的数列{an}共有3个:1 ,
, 1; 1,1,1; 1,2,1. …3分
(2)令bi=
(1≤i≤7),则对每个符合条件的数列{an},满足条件:bi∈{
, 1 , 2 }(1≤i≤7).
反之,由符合上述条件的7项数列{bn}可唯一确定一个符合条件的8项数列{an}.…7分
记符合条件的数列{bn}的个数为N.
显然,bi (1≤i≤7)中有k个2;从而有k个
,7-2k个1.
当k给定时,{bn}的取法有
种,易得k的可能值只有0,1,2,3,
故N=1+
+
+
=393.
因此,符合条件的数列{an}的个数为393. …10分.
因为
| a2 |
| a1 |
| 1 |
| 2 |
| a3 |
| a2 |
| 1 |
| 2 |
即a2∈{
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| 2 |
所以a2=
| 1 |
| 2 |
故此时满足条件的数列{an}共有3个:1 ,
| 1 |
| 2 |
(2)令bi=
| ai+1 |
| ai |
| 1 |
| 2 |
反之,由符合上述条件的7项数列{bn}可唯一确定一个符合条件的8项数列{an}.…7分
记符合条件的数列{bn}的个数为N.
显然,bi (1≤i≤7)中有k个2;从而有k个
| 1 |
| 2 |
当k给定时,{bn}的取法有
| C | k 7 |
| C | k 7-k |
故N=1+
| C | 1 7 |
| C | 1 6 |
| C | 2 7 |
| C | 2 5 |
| C | 3 7 |
| C | 3 4 |
因此,符合条件的数列{an}的个数为393. …10分.
点评:本题考查新定义,考查学生分析解决问题的能力,正确理解新定义是关键.

练习册系列答案
相关题目
 已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P. 为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.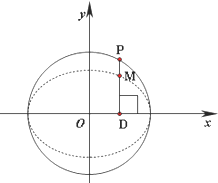 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且