题目内容
用lgx,lgy,lgz,lg(x+y),lg(x-y)表示下列各式:
lg(xyz),g(xy-2z-1,lg(x2y2z-3),lg(
÷y3z),lg(xy÷(x2-y2)),lg(((x+y)÷(x-y))×y),lg(
(x-y))2.
lg(xyz),g(xy-2z-1,lg(x2y2z-3),lg(
| x |
| y |
| x |
考点:对数的运算性质
专题:函数的性质及应用
分析:根据对数的运算法则与性质进行运算即可.
解答:
解:①lg(xyz)=lgx+lgy+lgz;
②lg(xy-2z-1)=lgx+lgy-2+lgz-1=lgx-2lgy-lgz;
③lg(x2y2z-3)=lgx2+lgy2+lgz-3=2lgx+2lgy-3lgz;
④lg(
÷y3z)=lg
-lg(y3z)=
lgx-3lgy-lgz;
⑤lg(xy÷(x2-y2))=lg(xy)-lg(x2-y2)=lgx+lgy-lg(x+y)-lg(x-y);
⑥lg(((x+y)÷(x-y))×y)=lg((x+y)÷(x-y))+lgy=lg(x+y)-lg(x-y)+lgy;
⑦lg(
(x-y))2=2lg(
(x-y))=2lg
+2lg(x-y)=2lgy-2lgx+2lg(x-y).
②lg(xy-2z-1)=lgx+lgy-2+lgz-1=lgx-2lgy-lgz;
③lg(x2y2z-3)=lgx2+lgy2+lgz-3=2lgx+2lgy-3lgz;
④lg(
| x |
| x |
| 1 |
| 2 |
⑤lg(xy÷(x2-y2))=lg(xy)-lg(x2-y2)=lgx+lgy-lg(x+y)-lg(x-y);
⑥lg(((x+y)÷(x-y))×y)=lg((x+y)÷(x-y))+lgy=lg(x+y)-lg(x-y)+lgy;
⑦lg(
| y |
| x |
| y |
| x |
| y |
| x |
点评:本题考查了对数的运算性质的应用问题,解题时应熟记对数的运算法则是什么,是基础题.

练习册系列答案
相关题目
已知S={1,2,3,…,21},A⊆S且A中有三个元素,若A中的元素可构成等差数列,则这样的集合A共有( )
| A、99个 | B、100个 |
| C、199个 | D、210个 |
设a=log5(2π),b=log5
,c=log6
( )
| 39 |
| 39 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、b>c>a |
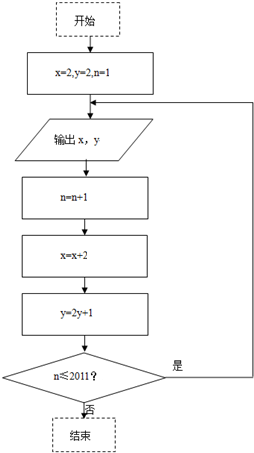 根据图所示的程序框图,将输出的x,y依次记为:x1,x2,…,x2011,y1,y2,…,y2011.
根据图所示的程序框图,将输出的x,y依次记为:x1,x2,…,x2011,y1,y2,…,y2011.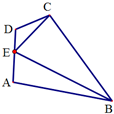 如图,在平面四边形ABCD中,DE=1.EC=
如图,在平面四边形ABCD中,DE=1.EC=