题目内容

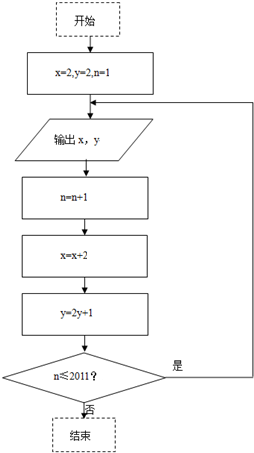根据图所示的程序框图，将输出的x，y依次记为：x1，x2，…，x2011，y1，y2，…，y2011．
（1）求出数列{xn}，{yn}的通项公式；
（2）求数列{xn+yn}（n≤2011）的前n项的和Sn．
考点：程序框图
专题：计算题,等差数列与等比数列,算法和程序框图
分析：（1）由程序框图，可得数列{xn}是以2为首项，2为公差的等差数列，数列{yn+1}是以3为首项，2为公比的等比数列，由此可求数列{xn}，{yn}，的通项公式；
（2）分组求和，结合等差数列、等比数列的求和公式，即可得到结论．
解答： 解：（1）由题意，x1=2，xn-xn-1=2（n≥2）
∴数列{xn}是以2为首项，2为公差的等差数列
∴xn=2+2（n-1）=2n；
由题意y1=2，yn=2yn-1+1（n≥2），∴yn+1=2（yn-1+1）
∴数列{yn+1}是以3为首项，2为公比的等比数列
∴yn+1=3•2n-1，yn=3•2n-1-1；
（2）数列{xn+yn}的前n项的和Sn=2（1+2+…+n）+3（1+2+…+2n-1）-n=3•2n+n2-3．
点评：本题考查等差数列、等比数列的判定，考查数列的求和公式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知
a
=（2，4，x）（x＞0），
b
=（2，y，2），若|
a
|=3
5
，且
a
⊥
b
，求x+2y的值．
设10x+y=6是函数f（x）=x3-2x2-9x+a（x＞
1
2
）的一条切线，则a=
 
．
已知f（x）=lnx-
a
x
（a∈R）
（1）若a＜0且f（x）在[1，e]的最小值为
3
2
，求a的值；
（2）若f（x）＜x2在（1，+∞）上恒成立，试求a的取值范围．
在空间直角坐标系中，点（1，0，2）关于坐标原点的对称点是
 
．
已知命题p：-2＜
1-a
3
＜a，命题q：集合A={x|x2+（a+2）x+1=0，x∈R}，B={x|x＞0}，且A∩B=∅．若命题p，q中有且只有一个为真命题，求实数a的取值范围．
已知向量
a
=（2sinx，cosx+sinx），
b
=（
3
cosx，sinx-cosx），定义f（x）=
a
•
b
．
（1）求函数f（x）的周期和单调递增区间；
（2）求函数f（x）的最大值及取得最大值时的x的取值集合；
（3）若函数y=2sin2x-1的图象向右平移m个单位（|m|＜
π
2
），向上平移n个单位后得到函数y=f（x）的图象，求实数m、n的值．
在平面直角坐标系xOy中，已知向量
OA
与
OB
关于y轴对称，向量
a
=（1，0），点A（x，y）满足不等式
OA2
+
a
•
AB
≤0，则x-y的取值范围（　　）
A、[
1-
2
2
，
1+
2
2
]
B、[1-
2
，1+
2
]
C、[-
2
2
，
2
2
]
D、[-
2
，
2
]
用lgx，lgy，lgz，lg（x+y），lg（x-y）表示下列各式：
lg（xyz），g（xy-2z-1，lg（x2y2z-3），lg（
x
÷y3z），lg（xy÷（x2-y2）），lg（（（x+y）÷（x-y））×y），lg（
y
x
（x-y））2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网