题目内容
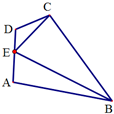如图，在平面四边形ABCD中，DE=1．EC=| 7 |
| 2π |
| 3 |
| π |
| 3 |
（1）CD；
（2）求cos∠AEB．
考点：余弦定理
专题：解三角形
分析：（1）在△CDE中，由余弦定理可得：EC2=DE2+DC2-2DE•DC•cos∠ED，解出即可．
（2）在△CDE中，由正弦定理可得：
=
，可得sin∠DEC\=
，∠DEC为锐角，可得cos∠DEC=
．设∠DEC=α．
利用cos∠AEB=cos(π-
-α)=cos
cosα+sin
sinα即可得出．
（2）在△CDE中，由正弦定理可得：
| DC |
| sin∠DEC |
| EC |
| sin∠CDE |
| DC•sin∠CDE |
| EC |
| 1-sin2∠DEC |
利用cos∠AEB=cos(π-
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
解答：
解：（1）在△CDE中，由余弦定理可得：EC2=DE2+DC2-2DE•DC•cos∠ED，
∴7=1+DC2-2DC×1×cos
，
化为DC2+DC-6=0，
解得DC=2．
（2）在△CDE中，由正弦定理可得：
=
，
∴sin∠DEC\=
=
=
．
∵∠DEC为锐角，∴cos∠DEC=
=
．
设∠DEC=α．
∴cos∠AEB=cos(π-
-α)=cos
cosα+sin
sinα
=-
×
+
×
=
．
∴7=1+DC2-2DC×1×cos
| 2π |
| 3 |
化为DC2+DC-6=0，
解得DC=2．
（2）在△CDE中，由正弦定理可得：
| DC |
| sin∠DEC |
| EC |
| sin∠CDE |
∴sin∠DEC\=
| DC•sin∠CDE |
| EC |
2×sin
| ||
|
| ||
| 7 |
∵∠DEC为锐角，∴cos∠DEC=
| 1-sin2∠DEC |
2
| ||
| 7 |
设∠DEC=α．
∴cos∠AEB=cos(π-
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=-
| 1 |
| 2 |
2
| ||
| 7 |
| ||
| 2 |
| ||
| 7 |
| ||
| 14 |
点评：本题考查了正弦定理与余弦定理、诱导公式、两角和差的余弦公式、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
在平面直角坐标系xOy中，已知向量
与
关于y轴对称，向量
=（1，0），点A（x，y）满足不等式
+
•
≤0，则x-y的取值范围（ ）
| OA |
| OB |
| a |
| OA2 |
| a |
| AB |
A、[
| ||||||||
B、[1-
| ||||||||
C、[-
| ||||||||
D、[-
|