题目内容
10.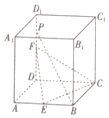 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.
分析 连结BD交CE于O,连结OF,则当BP∥OF时,PB∥平面CEF,推导出DP=3,四棱锥P-ABCD外接球就是三棱锥P-ABC的外接球,从而求出四棱锥P-ABCD外接球的半径,由此能求出四棱锥P-ABCD外接球的表面积.
解答 解:连结BD交CE于O,则$\frac{BO}{OD}$=$\frac{BE}{CD}$=$\frac{1}{2}$,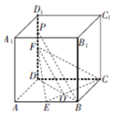
连结OF,则当BP∥OF时,PB∥平面CEF,则$\frac{PF}{FD}$=$\frac{1}{2}$,
∵F是DD1的中点,DD1=4,∴DP=3,
又四棱锥P-ABCD外接球就是三棱锥P-ABC的外接球,
∴四棱锥P-ABCD外接球的半径为:$\frac{\sqrt{{3}^{2}+{4}^{2}+{4}^{2}}}{2}$=$\frac{\sqrt{41}}{2}$.
外接球的表面积为:4$π×(\frac{\sqrt{41}}{2})^{2}$=41π.
故答案为:41π.
点评 本题考查四棱锥外接球的表面积的求法,考查正方体、四棱锥、球等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

练习册系列答案
相关题目
20.已知集合$A=\left\{{\left.{x∈Z}\right|\frac{4-x}{x+2}≥0}\right\}$,$B=\left\{{\left.x\right|\frac{1}{4}≤{2^x}≤4}\right\}$,则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {-2,-1,0,1,2} | D. | {0,1,2} |
1.(a+x)(1-x)4的展开式中x的奇数次幂项的系数之和为32,则a的值为( )
| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
18.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,左、右焦点分别为F1、F2,M为双曲线C的一条渐近线上某一点,且∠OMF2=$\frac{π}{2},{S_{△OM{F_2}}}=8\sqrt{3}$,则双曲线C的焦距为( )
| A. | $8\sqrt{3}$ | B. | 16 | C. | 8 | D. | $4\sqrt{3}$ |
15.过点(1,0)且与直线x+3y-5=0平行的直线方程是( )
| A. | x+3y+1=0 | B. | x+3y-1=0 | C. | 3x-y-3=0 | D. | 3x+y-3=0 |
19.分别在区间[1,6]和[1,4]内任取一个实数,依次记为x和y,则x<y的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{10}$ |
4.已知F1,F2为椭圆ax2+y2=4a(0<a<1)的两个焦点,A(0,2),点P为椭圆上任意一点,则|PA|-|PF2|的最小值是( )
| A. | a | B. | 2a | C. | 2$\sqrt{1-a}$-4 | D. | 2$\sqrt{2-a}$-4 |