题目内容
20.已知集合$A=\left\{{\left.{x∈Z}\right|\frac{4-x}{x+2}≥0}\right\}$,$B=\left\{{\left.x\right|\frac{1}{4}≤{2^x}≤4}\right\}$,则A∩B=( )| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {-2,-1,0,1,2} | D. | {0,1,2} |
分析 化简集合A、B,根据交集的定义写出A∩B.
解答 解:集合$A=\left\{{\left.{x∈Z}\right|\frac{4-x}{x+2}≥0}\right\}$={x∈Z|-2<x≤4}={-1,0,1,2,3,4},
$B=\left\{{\left.x\right|\frac{1}{4}≤{2^x}≤4}\right\}$={x|-2≤x≤2},
则A∩B={-1,0,1,2}.
故选:B.
点评 本题考查了集合的化简与运算问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.设函数F(x)=$\frac{f(x)}{e^x}$是定义在R上的函数,其中f(x)的导函数为f'(x),满足f'(x)<f(x)对于x∈R恒成立,则( )
| A. | f(2)>e2f(0),f(2 017>e2017f(0) | B. | f(2)>e2f(0),f(2 017)<e2017f(0) | ||
| C. | f(2)<e2f(0),f(2 017)>e2017f(0) | D. | f(2)<e2f(0),f(2 017)<e2017f(0) |
5.焦点为F的抛物线C:y2=8x的准线与x轴交于点A,点M在抛物线C上,则当$\frac{{|{MA}|}}{{|{MF}|}}$取得最大值时,直线MA的方程为( )
| A. | y=x+2或y=-x-2 | B. | y=x+2 | C. | y=2x+2或y=-2x+2 | D. | y=-2x+2 |
 如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.
如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.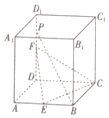 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.