题目内容
2.定义在R上的函数f(x)的反函数为f-1(x),且对任意的x都有f(x)+f(6-x)=2,则f-1(1)=( )| A. | 3 | B. | 2 | C. | 6 | D. | 4 |
分析 利用反函数与原函数的性质,即反函数的定义域是原函数的值域即可求解.
解答 解:任意的x都有f(x)+f(6-x)=2,
不妨设f-1(1)=M,
则f(M)=1,
那么:f(6-M)=1.
即f-1(1)=6-M,
可得:6-M=M,
∴M=3.
故得f-1(1)=3.
故选:A.
点评 本题考查反函数的定义,体现换元的数学思想,是基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
13.已知全集U=R,集合M=$\left\{{x|{{({\frac{1}{3}})}^x}≤1}\right\},N=\left\{{x|-1<x<4}\right\}$,则M∩N=( )
| A. | {x|-1<x≤0} | B. | {x|0≤x<4} | C. | {1,2,3} | D. | {0,1,2,3} |
17.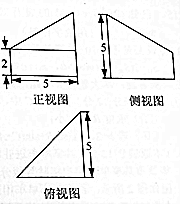 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )| A. | 50 | B. | 75 | C. | 25.5 | D. | 37.5 |
7.已知函数f(x)=$\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx(ω>0),将函数y=|f(x)|的图象向左平移$\frac{π}{9}$个单位长度后关于y轴对称,则当ω取最小值时,g(x)=cos(ωx+$\frac{π}{4}$)的单调递减区间为( )
| A. | [-$\frac{π}{3}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | B. | [-$\frac{π}{3}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) | ||
| C. | [-$\frac{π}{6}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | D. | [-$\frac{π}{6}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) |
14.设z=$\frac{10i}{3+i}$,则$\overline{z}$=( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
16.极坐标方程ρ=2cosθ-4sinθ对应的直角坐标方程为( )
| A. | (x-1)2+(y+2)2=5 | B. | (x-1)2+(y-2)2=5 | C. | (x-2)2+(y-1)2=5 | D. | (x+1)2+(y+2)2=5 |
 如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.
如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心.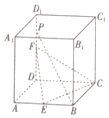 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.