题目内容
19.分别在区间[1,6]和[1,4]内任取一个实数,依次记为x和y,则x<y的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{10}$ |
分析 由题意知本题是一个几何概型,根据所给的条件作出试验发生是包含的所有事件是一个矩形区域,做出面积,看出满足条件的事件对应的面积,根据几何概型公式得到结果
解答  解:由题意,(x,y)表示的图形面积为(4-1)×(6-1)=15,其中满足x<y的图形面积为$\frac{1}{2}$×$3×3=\frac{9}{2}$,
解:由题意,(x,y)表示的图形面积为(4-1)×(6-1)=15,其中满足x<y的图形面积为$\frac{1}{2}$×$3×3=\frac{9}{2}$,
故x<y的概率为$\frac{\frac{9}{2}}{15}=\frac{3}{10}$.
故选B.
点评 本题考查了求概率;其中古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
7.已知函数f(x)=$\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx(ω>0),将函数y=|f(x)|的图象向左平移$\frac{π}{9}$个单位长度后关于y轴对称,则当ω取最小值时,g(x)=cos(ωx+$\frac{π}{4}$)的单调递减区间为( )
| A. | [-$\frac{π}{3}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | B. | [-$\frac{π}{3}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) | ||
| C. | [-$\frac{π}{6}$+$\frac{2kπ}{3}$,$\frac{π}{2}$+$\frac{2kπ}{3}$](k∈Z) | D. | [-$\frac{π}{6}$+$\frac{4kπ}{3}$,$\frac{π}{2}$+$\frac{4kπ}{3}$](k∈Z) |
14.设z=$\frac{10i}{3+i}$,则$\overline{z}$=( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
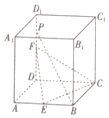 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的表面积为41π.