题目内容
如图，阴影部分的面积是 ．
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：确定积分区间与被积函数，求出原函数，即可求得定积分．
解答：
解：由
，可得交点坐标为（-3，6），（1，-2），
∴阴影部分的面积是S=
(-2x-x2+3)dx=（-x2-
x3+3x）
=
．
故答案为：
．
|
∴阴影部分的面积是S=
| ∫ | 1 -3 |
| 1 |
| 3 |
| | | 1 -3 |
| 32 |
| 3 |
故答案为：
| 32 |
| 3 |
点评：本题考查定积分求面积，考查导数知识的运用，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
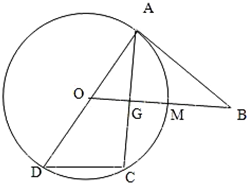如图所示，已知AD为圆O的直径，直线BA与圆O相切于点A，直线OB与弦AC垂直并相交于点G，与弧AC相交于M，连接DC，AB=10，AC=12，则BM=
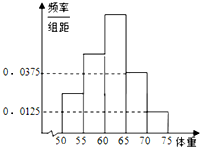为了了解高三学生的身体状况，抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图）．已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为15，则抽取的男生总人数是已知i是虚数单位，设复数z1=1-i，z2=1-2i，则z1•z2在复平面内对应点的坐标是（ ）
| A、（1，3） |
| B、（-1，3） |
| C、（-1，-3） |
| D、（3，-3） |