题目内容
函数f(x)=
+x的值域是( )
| 2x+1 |
| A、[0,+∞) | ||
B、[-
| ||
| C、[0,+∞) | ||
| D、[1,+∞) |
考点:函数的值域
专题:计算题,函数的性质及应用
分析:可得函数的定义域为[-
,+∞),函数单调递增,进而可得函数的最小值,可得值域.
| 1 |
| 2 |
解答:
解:由2x+1≥0可得x≥-
,
∴函数的定义域为:[-
,+∞),
又可得函数f(x)=
+x在[-
,+∞)上单调递增,
∴当x=-
时,函数取最小值f(-
)=-
,
∴函数f(x)=
+x的值域为:[-
,+∞),
故选B.
| 1 |
| 2 |
∴函数的定义域为:[-
| 1 |
| 2 |
又可得函数f(x)=
| 2x+1 |
| 1 |
| 2 |
∴当x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)=
| 2x+1 |
| 1 |
| 2 |
故选B.
点评:本题考查函数的值域,得出函数的单调性是解决问题的关键,属中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知集合M={x|-2<x<3},N={x|2x+1≥1},则M∩N等于( )
| A、(-2,-1] |
| B、(-2,1] |
| C、[1,3) |
| D、[-1,3) |
已知正方体的棱长为2
,则其外接球的表面积为( )
| 3 |
| A、48π | B、36π |
| C、32π | D、12π |
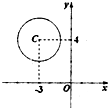 已知圆C:(x+3)2+(y-4)2=4
已知圆C:(x+3)2+(y-4)2=4