题目内容
14.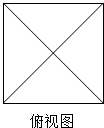 一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为$\sqrt{2}$,体积为$\frac{4\sqrt{2}}{3}$.
一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为$\sqrt{2}$,体积为$\frac{4\sqrt{2}}{3}$.
分析 根据正四棱锥的俯视图,可得到正四棱锥的直观图,然后根据正视图的定义得到正四棱锥的正视图,然后求面积体积即可.
解答  解:由正四棱锥的俯视图,可得到正四棱锥的直观图如图:
解:由正四棱锥的俯视图,可得到正四棱锥的直观图如图:
则该正四棱锥的正视图为三角形PEF,(E,F分别为AD.BC的中点)
∵正四棱锥的所有棱长均为2,
∴PB=PC=2,EF=AB=2,PF=$\sqrt{3}$,
∴PO=$\sqrt{P{F}^{2}-O{F}^{2}}$=$\sqrt{3-1}$=$\sqrt{2}$
∴该正四棱锥的正视图的面积为$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$;
正四棱锥的体积为$\frac{1}{3}$×2×2×$\sqrt{2}$=$\frac{4\sqrt{2}}{3}$.
故答案为:$\sqrt{2}$,$\frac{4\sqrt{2}}{3}$.
点评 本题主要考查三视图的应用,利用俯视图得到正四棱锥的直观图是解决本题的关键,比较基础.

练习册系列答案
相关题目
9.设a,b,c为三角形ABC三边,a≠1,b<c,若logc+ba+logc-ba=2logc+balog c-ba,则三角形ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
6.下列命题正确的是( )
| A. | 空间中两直线所成角的取值范围是:0°<θ≤90° | |
| B. | 直线与平面所成角的取值范围是:0°≤θ≤90° | |
| C. | 直线倾斜角的取值范围是:0°<θ≤180° | |
| D. | 两异面直线所成的角的取值范围是:0°<θ<90° |
4.已知函数f(x)=4x-2x+1-a没有零点,则实数a的取值范围是( )
| A. | a<-1 | B. | a≤0 | C. | a≥0 | D. | a≤-1 |