题目内容
19.${log_3}5+{log_5}\frac{1}{3}+{log_7}\root{3}{49}+\frac{1}{{{{log}_2}6}}+{log_5}3+{log_6}3-{log_3}15$=$\frac{2}{3}$.分析 根据对数的运算性质即可求出.
解答 解:${log_3}5+{log_5}\frac{1}{3}+{log_7}\root{3}{49}+\frac{1}{{{{log}_2}6}}+{log_5}3+{log_6}3-{log_3}15$=log3($\frac{5}{15}$)+log5($\frac{1}{3}$×3)+log7${7}^{\frac{2}{3}}$+log62+log63=-l+$\frac{2}{3}$+1=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了对数的运算性质,属于基础题.

练习册系列答案
相关题目
5.A≠∅是A∩B≠∅( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既是充分条件又是必要条件 | D. | 既不充分也不必要条件 |
7.若函数y=cosx+ax在[-$\frac{π}{2}$,$\frac{π}{2}$]存在递减区间,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,1) | C. | (-1,+∞) | D. | (1,+∞) |
4.已知两条直线l1:y=m和l2:y=$\frac{9}{m}$(m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2与函数y=|log2x|的图象从左至右相交于C,D.记线段AC和BD在x轴上的投影长度分别为a,b,当m变化时,$\frac{b}{a}$的最小值为( )
| A. | 32 | B. | $\frac{1}{64}$ | C. | 64 | D. | $\frac{1}{64}$ |
11.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4π | B. | $\frac{20π}{3}$ | C. | 12π | D. | 5π |
8.已知函数f(x)的定义域是(0,1),那么f(2x-1)的定义域是( )
| A. | (-∞,0) | B. | (0,2) | C. | ($\frac{1}{2}$,1) | D. | (1,+∞) |
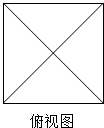 一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为$\sqrt{2}$,体积为$\frac{4\sqrt{2}}{3}$.
一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为$\sqrt{2}$,体积为$\frac{4\sqrt{2}}{3}$.