题目内容
9.设a,b,c为三角形ABC三边,a≠1,b<c,若logc+ba+logc-ba=2logc+balog c-ba,则三角形ABC的形状为( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 结合对数的运算性质,及换底公式的推论,可将已知化为:c2-b2=a2,再由勾股定理判断出三角形的形状.
解答 解:∵logc+ba+logc-ba=2logc+balog c-ba,
∴$\frac{1}{{log}_{c-b}a}$+$\frac{1}{{log}_{c+b}a}$=2,
即loga(c-b)+loga(c+b)=2,
∴loga(c2-b2)=2,
即c2-b2=a2,
故三角形ABC的形状为直角三角形,
故选:B.
点评 本题考查的知识点是三角形形状判断,对数的运算性质,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.某民营企业生产一种电子产品,2014年的产量在2013年的基础上增长率为a,2015年又在2014的基础上增长率为b(a>0,b>0)若这两年的平均增长率为q,则( )
| A. | q=$\frac{a+b}{2}$ | B. | q≥$\frac{a+b}{2}$ | ||
| C. | q≤$\frac{a+b}{2}$ | D. | q与$\frac{a+b}{2}$的大小关系不能确定 |
4.已知等差数列{an}的首项a1=1,公差d≠0,且a2是a1与a4的等比中项,则d=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
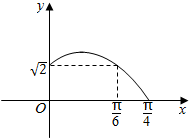 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.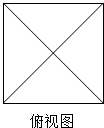 一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为$\sqrt{2}$,体积为$\frac{4\sqrt{2}}{3}$.
一个正四棱锥的所有棱长均为2,其俯视图如图所示,则该正四棱锥的正视图的面积为$\sqrt{2}$,体积为$\frac{4\sqrt{2}}{3}$.