题目内容
4．已知函数f（x）=4x-2x+1-a没有零点，则实数a的取值范围是（ ）| A． | a＜-1 | B． | a≤0 | C． | a≥0 | D． | a≤-1 |
分析 由题意可得a=4x-2x+1=（2x-1）2-1≥-1，从而求函数f（x）=4x-2x+1-a没有零点时实数a的取值范围．
解答 解：令4x-2x+1-a=0得，
a=4x-2x+1=（2x-1）2-1≥-1，
即a≥-1时，函数f（x）=4x-2x+1-a有零点，
故若函数f（x）=4x-2x+1-a没有零点，
则a＜-1；
故选：A．
点评 本题考查了函数的零点的判断与方程的解的应用．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
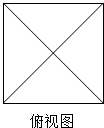一个正四棱锥的所有棱长均为2，其俯视图如图所示，则该正四棱锥的正视图的面积为$\sqrt{2}$，体积为$\frac{4\sqrt{2}}{3}$．
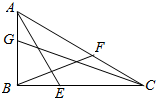如图，△ABC中，点E、F、G分别在边BC、AC、AB上，且$\frac{AG}{GB}$=$\frac{BE}{EC}$=$\frac{CF}{FA}$=$\frac{1}{2}$，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$．