题目内容
19．已知等差数列{an}的前n项和为Sn，公差d＜0，S11＞0，S12＜0．当Sn取得最大值时，n的值等于6．分析 由等差数列前n项和公式和通项公式得到a1+a11=2a6＞0，a6+a7＜0，从而得到a6＞0，a7＜0，由此能求出当Sn取得最大值时，n的值．
解答 解：∵等差数列{an}的前n项和为Sn，公差d＜0，S11＞0，S12＜0．
∴由题意：${S}_{11}=\frac{11}{2}（{a}_{1}+{a}_{11}）$＞0，①
${S}_{12}=\frac{12}{2}（{a}_{1}+{a}_{12}）$＜0，②
由①得a1+a11=2a6＞0，∴a6＞0，
由②得a1+a12＜0，∴a6+a7＜0，
∵a6＞0，∴a7＜0，
∴S6最大，∴当Sn取得最大值时，n的值等于6．
故答案为：6．
点评 本题考查等差数列前n项和取最大值时项数n的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
互动英语系列答案
相关题目
10．函数y=sin（2x-$\frac{π}{4}$）的图象可由函数y=cos2x的图象向左还是向右平移几个单位而得到（ ）
| A． | 向左、$\frac{π}{8}$单位 | B． | 向左、$\frac{π}{8}$单位 | C． | 向左、$\frac{3π}{8}$单位 | D． | 向右、$\frac{3π}{8}$单位 |
14．某民营企业生产一种电子产品，2014年的产量在2013年的基础上增长率为a，2015年又在2014的基础上增长率为b（a＞0，b＞0）若这两年的平均增长率为q，则（ ）
| A． | q=$\frac{a+b}{2}$ | B． | q≥$\frac{a+b}{2}$ | ||
| C． | q≤$\frac{a+b}{2}$ | D． | q与$\frac{a+b}{2}$的大小关系不能确定 |
8．已知cosα=$\frac{3}{5}$，且α是第四象限角，则tanα的值是（ ）
| A． | -$\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | -$\frac{4}{3}$ | D． | -$\frac{3}{4}$ |
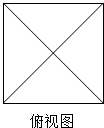一个正四棱锥的所有棱长均为2，其俯视图如图所示，则该正四棱锥的正视图的面积为$\sqrt{2}$，体积为$\frac{4\sqrt{2}}{3}$．