题目内容
17.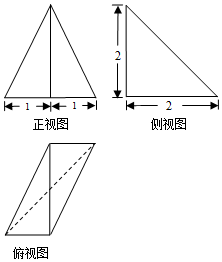 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
分析 如图所示,该几何体为三棱锥P-ABC.过点P作PO⊥平面ABC,垂足为O点,连接OB,OC,则四边形ABOC为平行四边形.OA⊥OB.
解答 解:如图所示,该几何体为三棱锥P-ABC.
过点P作PO⊥平面ABC,垂足为O点,连接OB,OC,则四边形ABOC为平行四边形.OA⊥OB.
则最长棱为PC=$\sqrt{{2}^{2}+{2}^{2}+{1}^{2}}$=3.
故选:C.
点评 本题考查了三棱锥的三视图、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知数列{an}满足a1=0,an+1=an+2n,那么a2009的值是( )
| A. | 2 008×2009 | B. | 2008×2007 | C. | 2009×2 010 | D. | 20092 |
5.已知F1、F2分别为双曲线C:$\frac{x^2}{4}-\frac{y^2}{5}$=1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
| A. | $\frac{4π}{15}$ | B. | $\frac{16π}{15}$ | C. | $\frac{64π}{15}$ | D. | $\frac{256π}{15}$ |
12. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积等于( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积等于( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积等于( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积等于( )| A. | $4\sqrt{3}π$ | B. | 3π | C. | 8π | D. | 12π |
2.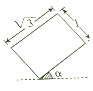 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )| A. | 2或3 | B. | 2$\sqrt{3}$或3 | C. | 1或3 | D. | 2或2$\sqrt{3}$ |
7.己知三棱锥A-BCO,OA,OB,OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在底面BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的O点所在的三个面所围成的几何体的表面积为( )
| A. | $\frac{5π}{2}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3+π}{2}$ | D. | 3+π |