题目内容

20．已知数列{an}满足a1=0，an+1=an+2n，那么a2009的值是（　　）
A．2 008×2009B．2008×2007C．2009×2 010D．20092

分析 由题意可知an+1-an=2n，a2009=a1+（a2-a1）+（a2-a3）+…+（a2009-a2008），根据等差数列的前n项和，即可求得a2009的值．

解答 解：由条件可知an+1-an=2n，则a2009=a1+（a2-a1）+（a2-a3）+…+（a2009-a2008）
=$0+2+4+…4016=\frac{2009（0+4016）}{2}$=2 008×2009．
故选A．

点评 本题考查数列的递推公式，考查等差数列前n项和公式，考查计算能力，属于中档题．

练习册系列答案
相关题目
10．在△ABC中，A=50°，AB=2，且△ABC的面积为$\frac{{\sqrt{3}}}{2}$，则BC的长为$\sqrt{4+\frac{3}{4si{n}^{2}50}-\frac{2\sqrt{3}cos50°}{sin50°}}$．
11．命题“?x∈N，x≥0”的否定是（　　）
A．?x∈N，x＜0B．?x∉N，x≥0C．?x∈N，x＜0D．?x∈N，x＞0
8．已知$\frac{π}{2}＜A＜π$，且sinA=$\frac{4}{5}$，那么sin2A等于（　　）
A．$\frac{24}{25}$B．$\frac{7}{25}$C．$-\frac{12}{25}$D．$-\frac{24}{25}$
15．已知向量$\overrightarrow{m}$=（2cos2x，$\sqrt{3}$），$\overrightarrow{n}$=（1，sin2x），设函数$f（x）=\overrightarrow m•\overrightarrow n$，则下列关于函数y=f（x）的性质的描述正确的是（　　）
A．关于直线$x=\frac{π}{12}$对称B．关于点$（{\frac{5π}{12}，0}）$对称
C．周期为2πD．y=f（x）在$（{-\frac{π}{3}，0}）$上是增函数
5．已知函数f（x）=$\frac{1}{2}$sin 2xsin φ+cos2xcos φ-$\frac{1}{2}$sin（$\frac{π}{2}$+φ）（0＜φ＜π），其图象过点（$\frac{π}{6}$，$\frac{1}{2}$）．
（1）求φ的值；
（2）求函数f（x）的单调增区间；
（3）将函数y=f（x）的图象上各点的横坐标缩短到原来的$\frac{1}{2}$，纵坐标不变，得到函数y=g（x）的图象，求函数g（x）在[0，$\frac{π}{4}$]上的最大值和最小值．
12．当m为何实数时，复数z=m2+m-2+（m2-1）i为
（1）实数；（2）虚数；（3）纯虚数．
16．已知函数f（x）=ax2-（a+2）x+lnx，其中a∈R．
（Ⅰ）当a=1时，求曲线y=f（x）的点（1，f（1））处的切线方程；
（Ⅱ）当a＞0时，若f（x）在区间[1，e]上的最小值为-2，求a的取值范围．
17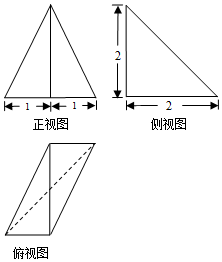．某三棱锥的三视图如图所示，则该三棱锥最长的棱长为（　　）
A．$\sqrt{5}$B．$2\sqrt{2}$C．3D．$3\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网