题目内容
7.己知三棱锥A-BCO,OA,OB,OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在底面BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的O点所在的三个面所围成的几何体的表面积为( )| A. | $\frac{5π}{2}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3+π}{2}$ | D. | 3+π |
分析 由于长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),有空间想象能力可知MN的中点P的轨迹为以O为球心,以1为半径的球体,即MN的中点P的轨迹与三棱锥的O点所在的三个面所围成的几何体为该球体的$\frac{1}{8}$,进而利用圆的面积公式及球体的表面积公式即可计算得解.
解答  解:因为长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),
解:因为长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),
由空间想象能力可知MN的中点P的轨迹为以O为球心,以1为半径的球体,
则MN的中点P的轨迹与三棱锥的O点所在的三个面所围成的几何体为该球体的$\frac{1}{8}$,
即:S=$\frac{1}{8}×4π×{1}^{2}$+$\frac{1}{4}$π×12×3=$\frac{5π}{4}$.
故选:B.
点评 此题考查了学生的空间想象能力,还考查了球体,三棱锥的面积公式的应用,考查了计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.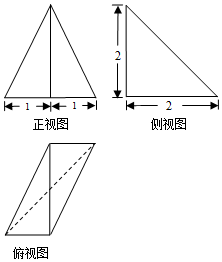 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
12.已知函数f(x)=$\left\{\begin{array}{l}{x+2,x>a}\\{{x}^{2}+5x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
19.数列{an}中,${a_{n+1}}+{(-1)^n}{a_n}=2n-1$,则数列{an}前16项和等于( )
| A. | 130 | B. | 132 | C. | 134 | D. | 136 |
16. 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{\sqrt{2}π}}{6}$ | C. | $12+\frac{2π}{3}$ | D. | $12+\frac{{\sqrt{2}π}}{6}$ |
17.已知点P为函数f(x)=lnx的图象上任意一点,点Q为圆${[{x-(e+\frac{1}{e})}]^2}+{y^2}=\frac{1}{4}$上任意一点,则线段PQ长度的最小值为( )
| A. | $\frac{{e-\sqrt{{e^2}-1}}}{e}$ | B. | $\frac{{2\sqrt{{e^2}+1}-e}}{2e}$ | C. | $\frac{{\sqrt{{e^2}+1}-e}}{2e}$ | D. | $e+\frac{1}{e}-\frac{1}{2}$ |
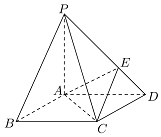 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;