题目内容
8.在平面直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆ρ=4cosθ与圆ρ=2sinθ交于O,A两点.(Ⅰ)求直线OA的斜率;
(Ⅱ)过O点作OA的垂线分别交两圆于点B,C,求|BC|.
分析 (Ⅰ)由由$\left\{\begin{array}{l}{ρ=2cosθ}\\{ρ=sinθ}\end{array}\right.$,得2cosθ=sinθ,化简即可得出kOA.
(Ⅱ)设A的极角为θ,tanθ=2,则sinθ=$\frac{2\sqrt{5}}{5}$,cosθ=$\frac{\sqrt{5}}{5}$,把B(ρ1,θ-$\frac{π}{2}$)代入ρ=2cosθ得ρ1.把C(ρ2,θ+$\frac{π}{2}$)代入ρ=sinθ得ρ2,利用|BC|=ρ1+ρ2,即可得出.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}{ρ=2cosθ}\\{ρ=sinθ}\end{array}\right.$,得2cosθ=sinθ,tanθ=2,
∴kOA=2.
(Ⅱ)设A的极角为θ,tanθ=2,则sinθ=$\frac{2\sqrt{5}}{5}$,cosθ=$\frac{\sqrt{5}}{5}$,则B(ρ1,θ-$\frac{π}{2}$),代入ρ=2cosθ得ρ1=2cos(θ-$\frac{π}{2}$)=2sinθ=$\frac{4\sqrt{5}}{5}$,
C(ρ2,θ+$\frac{π}{2}$),代代入ρ=sinθ得ρ2=sin(θ+$\frac{π}{2}$)=cosθ=$\frac{\sqrt{5}}{5}$,
∴|BC|=ρ1+ρ2=$\sqrt{5}$.
点评 本题考查了极坐标方程的应用、斜率计算、弦长计算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.命题“?x∈N,x≥0”的否定是( )
| A. | ?x∈N,x<0 | B. | ?x∉N,x≥0 | C. | ?x∈N,x<0 | D. | ?x∈N,x>0 |
3.设a>0,b>0,且a+b≤4,则有( )
| A. | $\frac{1}{ab}$≥$\frac{1}{2}$ | B. | $\frac{1}{a2+b2}$≤$\frac{1}{4}$ | C. | $\sqrt{ab}$≥2 | D. | $\frac{1}{a}$+$\frac{1}{b}$≥1 |
13.如图为某几何体的三视图,则其体积为( )


| A. | $\frac{14π}{6}+12$ | B. | $\frac{11π}{3}+4$ | C. | $\frac{11π}{6}+12$ | D. | $\frac{11π}{3}+12$ |
20.某四面体的三视图如图所示,该四面体的体积为( )


| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
17.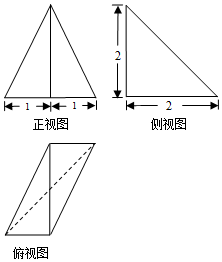 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
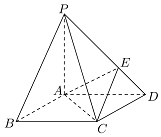 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;