题目内容
2.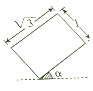 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )| A. | 2或3 | B. | 2$\sqrt{3}$或3 | C. | 1或3 | D. | 2或2$\sqrt{3}$ |
分析 根据正四棱柱的底面边长是1还是$\sqrt{3}$,分两种情况计算.
解答 解:由俯视图可知正四棱柱的底面边长为1,高为$\sqrt{3}$或底面边长为$\sqrt{3}$,高为1,
由俯视图可知主视图矩形的一边长为$\sqrt{3}$cosα+sinα=2sin(α+$\frac{π}{3}$),
(1)若正四棱柱的底面边长为1,高为$\sqrt{3}$,
则正视图的面积S=1•2sin(α+$\frac{π}{3}$)=2sin(α+$\frac{π}{3}$),
∴当α=$\frac{π}{6}$时,正视图的面积最大,最大面积为2.
(2)若正四棱柱的底面边长为$\sqrt{3}$,高为1,
则正视图的面积S=$\sqrt{3}$•2sin(α+$\frac{π}{3}$)=2$\sqrt{3}$sin(α+$\frac{π}{3}$),
∴当α=$\frac{π}{6}$时,正视图的面积最大,最大面积为2$\sqrt{3}$.
故选D.
点评 本题考查了棱柱的三视图,属于中档题.

练习册系列答案
相关题目
13.如图为某几何体的三视图,则其体积为( )


| A. | $\frac{14π}{6}+12$ | B. | $\frac{11π}{3}+4$ | C. | $\frac{11π}{6}+12$ | D. | $\frac{11π}{3}+12$ |
10.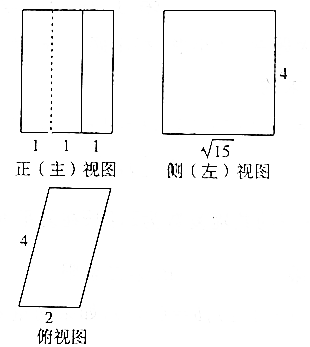 如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )
 如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,俯视图是平行四边形,则该几何体的体积是( )| A. | $\frac{8\sqrt{15}}{3}$ | B. | 8$\sqrt{15}$ | C. | $\frac{4\sqrt{15}}{3}$ | D. | 4$\sqrt{15}$ |
17.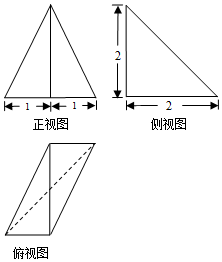 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
7.一汽车销售公司对开业5年来某种型号的汽车“五一”优惠金额与销售量之间的关系进行分析研究并做了记录,得到如下资料.
该公司所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1年与第5年的两组数据,请根据其余三年的数据,求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2辆,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
相关公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 日期 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 优惠金额x(千元) | 10 | 11 | 13 | 12 | 8 |
| 销售量y(辆) | 23 | 25 | 30 | 26 | 16 |
(1)若选取的是第1年与第5年的两组数据,请根据其余三年的数据,求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2辆,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
相关公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
11.某乳业公司生产甲、乙两种产品,需要A、B、C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如表所示:
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
| 产品苜蓿草饲料 | A | B | C |
| 甲 | 4 | 8 | 3 |
| 乙 | 5 | 5 | 10 |
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
12.已知函数f(x)=$\left\{\begin{array}{l}{x+2,x>a}\\{{x}^{2}+5x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |