题目内容
12．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积等于（ ）| A． | $4\sqrt{3}π$ | B． | 3π | C． | 8π | D． | 12π |
分析 作出棱锥的直观图，根据棱锥的结构特征得出外接球的球心位置，再计算球的表面积．
解答 解：作出几何体的三视图如图所示：
其中PA⊥平面ABC，AB⊥BC，PA=AB=BC=2，
∴PB=2$\sqrt{2}$，PC=2$\sqrt{3}$，
∵三棱锥的各侧面均为直角三角形，
∴PC为棱锥外接球的直径，
∴外接球的表面积S=4π×（$\frac{2\sqrt{3}}{2}$）2=12π．
故选D．
点评 本题考查了棱锥与外接球的位置关系，几何体的面积计算，属于中档题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
15．已知向量$\overrightarrow{m}$=（2cos2x，$\sqrt{3}$），$\overrightarrow{n}$=（1，sin2x），设函数$f（x）=\overrightarrow m•\overrightarrow n$，则下列关于函数y=f（x）的性质的描述正确的是（ ）
| A． | 关于直线$x=\frac{π}{12}$对称 | B． | 关于点$（{\frac{5π}{12}，0}）$对称 | ||
| C． | 周期为2π | D． | y=f（x）在$（{-\frac{π}{3}，0}）$上是增函数 |
3．设a＞0，b＞0，且a+b≤4，则有（ ）
| A． | $\frac{1}{ab}$≥$\frac{1}{2}$ | B． | $\frac{1}{a2+b2}$≤$\frac{1}{4}$ | C． | $\sqrt{ab}$≥2 | D． | $\frac{1}{a}$+$\frac{1}{b}$≥1 |
20．某四面体的三视图如图所示，该四面体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | 2 | C． | $\frac{8}{3}$ | D． | 4 |
17．
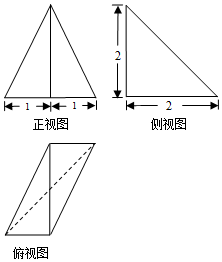某三棱锥的三视图如图所示，则该三棱锥最长的棱长为（ ）
某三棱锥的三视图如图所示，则该三棱锥最长的棱长为（ ）| A． | $\sqrt{5}$ | B． | $2\sqrt{2}$ | C． | 3 | D． | $3\sqrt{2}$ |