题目内容
6.已知{an}为等差数列,Sn为其前n项和,若a1=8,a4+a6=0,则S8=8.分析 利用等差数列的通项公式与求和公式即可得出.
解答 解:设等差数列{an}的公差为d,∵a1=8,a4+a6=0,
∴2×8+8d=0,解得d=-2.
则S8=8×8-2×$\frac{8×7}{2}$=8.
故答案为:8.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.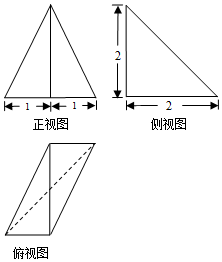 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )
某三棱锥的三视图如图所示,则该三棱锥最长的棱长为( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
11.某乳业公司生产甲、乙两种产品,需要A、B、C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如表所示:
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
| 产品苜蓿草饲料 | A | B | C |
| 甲 | 4 | 8 | 3 |
| 乙 | 5 | 5 | 10 |
已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;
(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
16. 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{\sqrt{2}π}}{6}$ | C. | $12+\frac{2π}{3}$ | D. | $12+\frac{{\sqrt{2}π}}{6}$ |
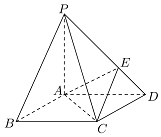 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1;