题目内容
动点P在函数y=sin2x的图象上移动，动点Q（x，y）满足
=（
，0），则动点Q的轨迹方程为（ ）
| PQ |
| π |
| 8 |
A、y=sin（2x+
| ||
B、y=sin（2x-
| ||
C、y=sin（2x+
| ||
D、y=sin（2x-
|
考点：轨迹方程,函数y=Asin（ωx+φ）的图象变换
专题：函数的性质及应用,三角函数的图像与性质
分析：设出P的坐标，利用
=（
，0），直接求出动点Q的轨迹方程．
| PQ |
| π |
| 8 |
解答：
解：设P（a，b），∵
=（
，0），动点Q（x，y）
∴x-a=
，y-b=0，可得
，
∵动点P在函数y=sin2x的图象上移动，
∴y=sin2（x-
）=sin（2x-
），
动点Q的轨迹方程为y=sin（2x-
）．
故选：D．
| PQ |
| π |
| 8 |
∴x-a=
| π |
| 8 |
|
∵动点P在函数y=sin2x的图象上移动，
∴y=sin2（x-
| π |
| 8 |
| π |
| 4 |
动点Q的轨迹方程为y=sin（2x-
| π |
| 4 |
故选：D．
点评：本题考查轨迹方程的求法，相关点方法的应用，考查计算能力．
练习册系列答案
相关题目
以下有关命题的说法错误的是（ ）
| A、命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0” | ||||||
B、“cosα=-
| ||||||
| C、对于命题p：?x∈R，使得x2+x+1＜0，则￢p：?x∈R，则x2+x+1≥0 | ||||||
| D、若p∧q为假命题，则p、q均为假命题 | ||||||
| E、对于命题p：?x∈R，使得x2+x+1＜0，则￢p：?x∈R，则x2+x+1≥0 |
已知全集U=R，集合A={x|-1≤x＜3}，B={0，2，4，6}，则A∩B等于（ ）
| A、{0，2} |
| B、{-1，0，2} |
| C、{x|0≤x≤2} |
| D、{x|-1≤x≤2} |
“函数y=sin（x+φ）为偶函数”是“φ=
”的（ ）
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设a＞0，且a≠1，则“函数y=logax在（0，+∞）上是减函数”是“函数y=（2-a）x3在R上是增函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在平面直角坐标系中，x轴的正半轴上有4个点，y轴的正半轴上有5个点，这9个点任意两点连线，则所有连线段的交点落入第一象限的个数最多是（ ）
| A、30 | B、60 |
| C、120 | D、240 |
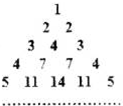用部分自然数构造如图的数表：用aij（i≥j）表示第i行第j个数（i，j∈N+），使得ai1=aij=i．每行中的其他各数分别等于其“肩膀”上的两个数之和．设第n（n∈N+）行中的各数之和为bn．