题目内容
设a＞0，且a≠1，则“函数y=logax在（0，+∞）上是减函数”是“函数y=（2-a）x3在R上是增函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据函数单调性的性质，利用充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若函数y=logax在（0，+∞）上是减函数，则0＜a＜1，
此时2-a＞0，函数y=（2-a）x3在R上是增函数，成立．
若y=（2-a）x3在R上是增函数，则2-a＞0，即a＜2，
当1＜a＜2时，函数y=logax在（0，+∞）上是增函数，∴函数y=logax在（0，+∞）上是减函数不成立，
即“函数y=logax在（0，+∞）上是减函数”是“函数y=（2-a）x3在R上是增函数”的充分而不必要条件，
故选：A．
此时2-a＞0，函数y=（2-a）x3在R上是增函数，成立．
若y=（2-a）x3在R上是增函数，则2-a＞0，即a＜2，
当1＜a＜2时，函数y=logax在（0，+∞）上是增函数，∴函数y=logax在（0，+∞）上是减函数不成立，
即“函数y=logax在（0，+∞）上是减函数”是“函数y=（2-a）x3在R上是增函数”的充分而不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的判断，利用函数单调性的性质是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）=x2+ax，x∈R，常数a∈R，则（ ）
| A、存在a，使f（x）是奇函数 |
| B、存在a，使f（x）是偶函数 |
| C、?a∈R，f（x）在（0，+∞）上是增函数 |
| D、?a∈R，f（x）在（-∞，0）上是减函数 |
设函数f（x）=sin（2x+
），则下列结论正确的是（ ）
| π |
| 3 |
A、f（x）的图象关于直线x=
| ||
B、f（x）的图象关于点（
| ||
C、f（x）的最小正周期为
| ||
D、f（x）在[0，
|
动点P在函数y=sin2x的图象上移动，动点Q（x，y）满足
=（
，0），则动点Q的轨迹方程为（ ）
| PQ |
| π |
| 8 |
A、y=sin（2x+
| ||
B、y=sin（2x-
| ||
C、y=sin（2x+
| ||
D、y=sin（2x-
|
将5名实习教师分配到高一年级的3个班实习，每班至少1名，则不同的分配方案有（ ）
| A、30种 | B、60种 |
| C、90种 | D、150种 |
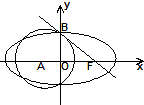如图，已知点F为椭圆C：