题目内容
已知全集U=R，集合A={x|-1≤x＜3}，B={0，2，4，6}，则A∩B等于（ ）
| A、{0，2} |
| B、{-1，0，2} |
| C、{x|0≤x≤2} |
| D、{x|-1≤x≤2} |
考点：交集及其运算
专题：集合
分析：根据A与B，找出A与B的交集即可．
解答：
解：∵A={x|-1≤x＜3}，B={0，2，4，6}，
∴A∩B={0，2}．
故选：A．
∴A∩B={0，2}．
故选：A．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
相关题目
若函数f（x）=x2+ax，x∈R，常数a∈R，则（ ）
| A、存在a，使f（x）是奇函数 |
| B、存在a，使f（x）是偶函数 |
| C、?a∈R，f（x）在（0，+∞）上是增函数 |
| D、?a∈R，f（x）在（-∞，0）上是减函数 |
执行如图所示的程序框图，如果输入a=1，b=2，则输出的a的值为（ ）
| A、7 | B、9 | C、11 | D、13 |
设函数f（x）=sin（2x+
），则下列结论正确的是（ ）
| π |
| 3 |
A、f（x）的图象关于直线x=
| ||
B、f（x）的图象关于点（
| ||
C、f（x）的最小正周期为
| ||
D、f（x）在[0，
|
动点P在函数y=sin2x的图象上移动，动点Q（x，y）满足
=（
，0），则动点Q的轨迹方程为（ ）
| PQ |
| π |
| 8 |
A、y=sin（2x+
| ||
B、y=sin（2x-
| ||
C、y=sin（2x+
| ||
D、y=sin（2x-
|
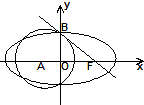如图，已知点F为椭圆C：