题目内容
函数f(x)和g(x)的定义域为R,且f(x)为偶函数,g(x)为奇函数,f(x)+g(x)=
,则F(x)=
在定义域内的增区间为( )
| 1 |
| x2-x+1 |
| f(x) |
| g(x) |
| A、(-∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)和(1,+∞) |
| D、(-∞,+∞) |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:利用f(x)是偶函数,g(x)是奇函数,列出方程组求f(x)和g(x)的解析式,然后代入F(x)=
,化简,求定义域,求增区间.
| f(x) |
| g(x) |
解答:
解:∵f(x)是偶函数,g(x)是奇函数,
∴f(-x)=f(x),g(-x)=-g(x)
又∵f(x)+g(x)=
①,
∴f(-x)+g(-x)=f(x)-g(x)=
②,
①②联立可解得f(x)=
,g(x)=
,
则F(x)=
=
,函数的定义域为{x|x≠0},
∵F(x)=
=
(x+
),
∴F′(x)=
(1-
),
令F′(x)=
(1-
)>0,解得x<-1或x>1,
则F(x)=
在定义域内的增区间为(-∞,-1)和(1,+∞).
∴f(-x)=f(x),g(-x)=-g(x)
又∵f(x)+g(x)=
| 1 |
| x2-x+1 |
∴f(-x)+g(-x)=f(x)-g(x)=
| 1 |
| x2+x+1 |
①②联立可解得f(x)=
| x2+1 |
| (x2-x+1)(x2+x+1) |
| 2x |
| (x2-x+1)(x2+x+1) |
则F(x)=
| f(x) |
| g(x) |
| x2+1 |
| 2x |
∵F(x)=
| x2+1 |
| 2x |
| 1 |
| 2 |
| 1 |
| x |
∴F′(x)=
| 1 |
| 2 |
| 1 |
| x2 |
令F′(x)=
| 1 |
| 2 |
| 1 |
| x2 |
则F(x)=
| f(x) |
| g(x) |
点评:本题考查函数的奇偶性,单调性以及函数的定义域,考查计算能力,属于中档题目.

练习册系列答案
相关题目
定义域为R的函数f(x),对?x都有f(x)=f(2-x),则下列选项一定正确的是( )
| A、f(-x)为偶函数 |
| B、f(x-1)为偶函数 |
| C、f(1-x)为偶函数 |
| D、f(x-2)为偶函数 |
函数f(x)=log2x-3sin
x的零点个数是( )
| π |
| 2 |
| A、3 | B、4 | C、5 | D、7 |
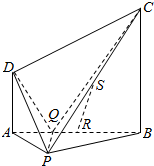 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.