题目内容
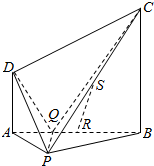 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.(Ⅰ)求证:①平面PAD⊥平面PBC;②RS∥平面PAD;
(Ⅱ)若点Q在线段AB上,且CD⊥平面PDQ,求二面角C-PQ-D的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)①由已知得AD⊥平面APB,从而PB⊥AD,由此能证明平面PAD⊥平面PBC.
②取PB中点M,连结RM,SM,由已知推导出平面PAD∥平面SMR,由此能证明RS∥平面PAD.
(Ⅱ)由已知得AP=1,BP=
,PQ=
,AQ=
,BQ=
,以Q为原点,QP为x轴,QB为y轴,建立如图所示的空间直角坐标系,利用向量法能求出二面角C-PQ-D的余弦值.
②取PB中点M,连结RM,SM,由已知推导出平面PAD∥平面SMR,由此能证明RS∥平面PAD.
(Ⅱ)由已知得AP=1,BP=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
(Ⅰ)①证明:∵在四棱锥P-ABCD中,底面ABCD是直角梯形,
平面PAB⊥平面ABCD,AD⊥AB,
∴AD⊥平面APB,
又PB?平面APB,
∴PB⊥AD,
∵PD⊥PB,AD∩PD=D,
∴PB⊥平面PAD,
∵PB?平面PBC,
∴平面PAD⊥平面PBC.
②证明:取PB中点M,连结RM,SM,
∵R、S分别是棱AB、PC的中点,AD∥BC,
∴SM∥CB∥AD,RM∥AP,
又AD∩AP=A,∴平面PAD∥平面SMR,
∵RS?平面SMR,∴RS∥平面PAD.
(Ⅱ)解:由已知得
,
解得AP=1,BP=
,PQ=
,AQ=
,BQ=
,
以Q为原点,QP为x轴,QB为y轴,建立如图所示的空间直角坐标系,
则Q(0,0,0),P(
,0,0),D(0,-
,1),C(0,
,2),
∴
=(0,-
,1),
=(
,0,0),
=(0,
,2),
设平面PDQ的法向量
=(x,y,z),
则
,取y=2,得
=(0,2,1),
设平面PCQ的法向量
=(a,b,c),
则
,取b=4,得
=(0,4,-3),
设二面角C-PQ-D的平面角为θ,
∴cosθ=|cos<
,
>|=|
|=
,
∴二面角C-PQ-D的余弦值为
.

平面PAB⊥平面ABCD,AD⊥AB,
∴AD⊥平面APB,
又PB?平面APB,
∴PB⊥AD,
∵PD⊥PB,AD∩PD=D,
∴PB⊥平面PAD,
∵PB?平面PBC,
∴平面PAD⊥平面PBC.
②证明:取PB中点M,连结RM,SM,
∵R、S分别是棱AB、PC的中点,AD∥BC,
∴SM∥CB∥AD,RM∥AP,
又AD∩AP=A,∴平面PAD∥平面SMR,
∵RS?平面SMR,∴RS∥平面PAD.
(Ⅱ)解:由已知得
|
解得AP=1,BP=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
以Q为原点,QP为x轴,QB为y轴,建立如图所示的空间直角坐标系,
则Q(0,0,0),P(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| QD |
| 1 |
| 2 |
| QP |
| ||
| 2 |
| QC |
| 3 |
| 2 |
设平面PDQ的法向量
| n |
则
|
| n |
设平面PCQ的法向量
| m |
则
|
| m |
设二面角C-PQ-D的平面角为θ,
∴cosθ=|cos<
| m |
| n |
| 8-3 | ||
|
| ||
| 5 |
∴二面角C-PQ-D的余弦值为
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
函数f(x)和g(x)的定义域为R,且f(x)为偶函数,g(x)为奇函数,f(x)+g(x)=
,则F(x)=
在定义域内的增区间为( )
| 1 |
| x2-x+1 |
| f(x) |
| g(x) |
| A、(-∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)和(1,+∞) |
| D、(-∞,+∞) |
函数f(x)=ax3+bx2-3x在x=±1处取得极值,则f(x)的极大值是( )
| A、2 | B、4 | C、6 | D、8 |
直线x+y-1=0被圆x2+y2-2x-2y-6=0所截得弦的中点坐标是( )
| A、(1,0) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
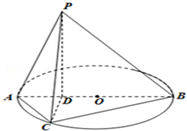 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD= 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.