题目内容
在椭圆
+
=1上求一点P，使其到直线l：3x-2y-16=0的距离最短．
| x2 |
| 4 |
| y2 |
| 7 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由P在椭圆7x2+4y2=28上，求点P到直线3x-2y-16=0的距离的最小值，对称平行线方程，利用直线与椭圆相切由此能求出点P到直线3x-2y-16=0的距离的最小值．并且求出切点坐标．
解答：
解：椭圆
+
=1化为7x2+4y2=28，P在椭圆7x2+4y2=28上，
点P到直线3x-2y-16=0的距离的最小值，转化为平行线与椭圆相切时，平行线之间的距离，设平行线方程为：3x-2y+m=0，与椭圆联立可得：16x2+6mx-28+m2=0，平行线与椭圆相切，所以△=0，
可得36m2-4×16（m2-28）=0．
，解得m=±8，m=-8时，满足题意．此时P的横坐标x=
，纵坐标为：y=-
．
所求P的坐标(
，-
)．
| x2 |
| 4 |
| y2 |
| 7 |
点P到直线3x-2y-16=0的距离的最小值，转化为平行线与椭圆相切时，平行线之间的距离，设平行线方程为：3x-2y+m=0，与椭圆联立可得：16x2+6mx-28+m2=0，平行线与椭圆相切，所以△=0，
可得36m2-4×16（m2-28）=0．
，解得m=±8，m=-8时，满足题意．此时P的横坐标x=
| 3 |
| 2 |
| 7 |
| 4 |
所求P的坐标(
| 3 |
| 2 |
| 7 |
| 4 |
点评：本题考查直线与椭圆的位置关系，解题时要认真审题，注意椭圆的参数方程、点到直线的距离公式、三角函数的性质的灵活运用．
练习册系列答案
相关题目
函数f（x）和g（x）的定义域为R，且f（x）为偶函数，g（x）为奇函数，f（x）+g（x）=
，则F（x）=
在定义域内的增区间为（ ）
| 1 |
| x2-x+1 |
| f(x) |
| g(x) |
| A、（-∞，-1） |
| B、（1，+∞） |
| C、（-∞，-1）和（1，+∞） |
| D、（-∞，+∞） |
如图由若干个相同的小立方体组成的几何体的俯视图，其中小立方体中的数字表示相应位置的小立方体的个数，则该几何体的左视图为（ ）
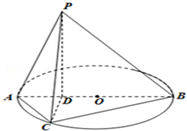如图所示，已知PD垂直以AB为直径的圆O所在平面，点D在线段AB上，点C为圆O上一点，且BD=