题目内容
给出下列五个命题:
①函数y=
+
是偶函数,但不是奇函数;
②函数y=tanx的图象关于点(
,0)对称;
③正弦函数在第一象限为增函数;
④方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
⑤函数f(x)=loga(6-ax)(a>0且a≠1)在[0,2]上为减函数,则1<a<3.
其中正确的个数( )
①函数y=
| x2-1 |
| 1-x2 |
②函数y=tanx的图象关于点(
| π |
| 2 |
③正弦函数在第一象限为增函数;
④方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0;
⑤函数f(x)=loga(6-ax)(a>0且a≠1)在[0,2]上为减函数,则1<a<3.
其中正确的个数( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①根据函数奇偶性的定义进行判断,
②根据正切函数的图象进行判断;
③根据正弦函数的单调性进行判断,
④根据根与系数之间的关系进行判断;
⑤根据复合函数单调性之间的关系进行判断.
②根据正切函数的图象进行判断;
③根据正弦函数的单调性进行判断,
④根据根与系数之间的关系进行判断;
⑤根据复合函数单调性之间的关系进行判断.
解答:
解:①由
,即
,解得x=±1,则f(x)=0,即f(x)是既是奇函数也是偶函数,故①错误;
②函数y=tanx的图象关于点(
,0)对称,正确;
③正弦函数在第一象限不是增函数,故②错误;
④若方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则
,解得a<0,故④正确;
⑤函数f(x)=loga(6-ax)(a>0且a≠1)在[0,2]上为减函数,则满足
,
即
,则1<a<3.故⑤正确,
故选:C
|
|
②函数y=tanx的图象关于点(
| π |
| 2 |
③正弦函数在第一象限不是增函数,故②错误;
④若方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则
|
⑤函数f(x)=loga(6-ax)(a>0且a≠1)在[0,2]上为减函数,则满足
|
即
|
故选:C
点评:本题主要考查各种命题的真假判断,根据函数的性质是解决本题的关键.综合性较强.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
函数f(x)和g(x)的定义域为R,且f(x)为偶函数,g(x)为奇函数,f(x)+g(x)=
,则F(x)=
在定义域内的增区间为( )
| 1 |
| x2-x+1 |
| f(x) |
| g(x) |
| A、(-∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)和(1,+∞) |
| D、(-∞,+∞) |
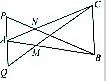 在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量
在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量