题目内容
定义域为R的函数f(x),对?x都有f(x)=f(2-x),则下列选项一定正确的是( )
| A、f(-x)为偶函数 |
| B、f(x-1)为偶函数 |
| C、f(1-x)为偶函数 |
| D、f(x-2)为偶函数 |
考点:奇偶函数图象的对称性
专题:规律型,函数的性质及应用
分析:先由题干得出函数f(x)图形关于直线x=1对称,在联系4个选项可以看出题目考察偶函数,图象关于y轴对称的函数是偶函数,由函数图象平移知识可得答案.
解答:
解:定义域为R的函数f(x),对?x都有f(x)=f(2-x),则函数图形关于直线x=1对称,
4个选项中考察为偶函数的,也就是图象关于y轴即x=0对称的,
将原函数图象向左平移1个单位就会关于x=0对称,即f(x+1)为偶函数,
因此f(x+1)的图象关于y轴对称,又f(x+1)为偶函数,
有偶函数性质f(-x)=f(x)得f(x+1)=f(-x+1),即f(-x+1)也是偶函数,
故选:C.
4个选项中考察为偶函数的,也就是图象关于y轴即x=0对称的,
将原函数图象向左平移1个单位就会关于x=0对称,即f(x+1)为偶函数,
因此f(x+1)的图象关于y轴对称,又f(x+1)为偶函数,
有偶函数性质f(-x)=f(x)得f(x+1)=f(-x+1),即f(-x+1)也是偶函数,
故选:C.
点评:本题考查函数的对称性和函数图象的平移,关键是转化为对称和平移求解,属于规律型题目,要注意总结.

练习册系列答案
相关题目
如图所示的程序框图输出的结果b=( )


| A、7 | B、9 | C、11 | D、13 |
函数f(x)和g(x)的定义域为R,且f(x)为偶函数,g(x)为奇函数,f(x)+g(x)=
,则F(x)=
在定义域内的增区间为( )
| 1 |
| x2-x+1 |
| f(x) |
| g(x) |
| A、(-∞,-1) |
| B、(1,+∞) |
| C、(-∞,-1)和(1,+∞) |
| D、(-∞,+∞) |
函数f(x)=ax3+bx2-3x在x=±1处取得极值,则f(x)的极大值是( )
| A、2 | B、4 | C、6 | D、8 |
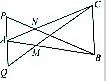 在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量
在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量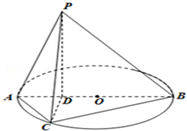 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=