Question

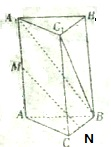如图所示，三棱柱A₁B₁C₁-ABC的底面是边长为1的正三角形，侧棱A₁A⊥底面ABC且A₁A=2，M、N分别为AA₁、BC的中点．
（1）求证：MN∥平面A₁BC₁；
（2）求直线MN与BC₁所成角的余弦值．

Answer 1

考点：异面直线及其所成的角,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）首先利用面面平行的判定求出平面MNG∥平面A₁BC₁，进一步转化成线面平行．
（2）首先利用平行线得到异面直线的夹角的平面角，进一步通过解三角形知识求出结果．

解答： 证明：（1）在三棱柱A₁B₁C₁-ABC中，取AB的中点G，连接GN和MG，
由于M、N分别为AA₁、BC的中点．G是AB的中点．
所以：MG∥A₁B，NG∥AC，AC∥A₁C₁
MG和NG是相交直线，A₁B和A₁C₁是相交直线．
则：平面MNG∥平面A₁BC₁
所以：MN∥平面A₁BC₁
解：（2）在三棱柱A₁B₁C₁-ABC中，取CC₁的中点H，连接NH和MH，
所以：直线MN与BC₁所成角即直线MN和NH所成的角．
三棱柱A₁B₁C₁-ABC的底面是边长为1的正三角形，侧棱A₁A⊥底面ABC且A₁A=2，
M、N分别为AA₁、BC的中点．
所以求得：NH=

5

2

，MH=1，MN=

7

2

在△MNH中，由于MN²=MH²+NH²，
所以△MNH是直角三角形．
所以：cos∠HNM=

NH

MN

=

35

7

即直线直线MN与BC₁所成角的余弦值为

35

7

．

点评：本题考查的知识要点：面面平行的判定，线面平行的判定，异面直线的夹角的应用及相关的运算．属于基础题型．