题目内容
从集合{-1,1,2}中随机选取一个数记为m,从集合{-1,2}中随机选取一个数记为n,则方程
+
=1表示双曲线的概率为 .
| x2 |
| m |
| y2 |
| n |
考点:列举法计算基本事件数及事件发生的概率,双曲线的标准方程
专题:概率与统计
分析:先写出总的基本事件数,在由双曲线的方程特点需mn<0,只需列举出符合条件的基本事件即可.
解答:
解:由题意知基本事件总数为3×2=6,
表示双曲线的要求为:mn<0.
当m=-1时,n=2;当n=-1时,m=1、2,共3种情况.
故表示双曲线的概率为:P=
=
,
故答案为
.
表示双曲线的要求为:mn<0.
当m=-1时,n=2;当n=-1时,m=1、2,共3种情况.
故表示双曲线的概率为:P=
| 3 |
| 6 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题为古典概型的求解,涉及双曲线的标准方程的特点,属基础题.

练习册系列答案
相关题目
阅读如图的程序框图,运行相应的程序,则输出S的值为( )


| A、8 | B、18 | C、26 | D、80 |
下列函数为奇函数的是( )
A、y=x
| ||
| B、y=lgx2 | ||
| C、1og2x | ||
D、y=2x-
|
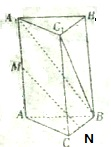 如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.
如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.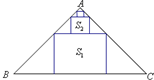 在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则
在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则