题目内容
已知x∈R,则函数f(x)=
-
的值域是 .
| x2+x+1 |
| x2-x+1 |
考点:函数的值域
专题:函数的性质及应用
分析:配方由两点间的距离公式可得f(x)的值域表示|PA|-|PB|的取值范围,由三角形的三边关系可得.
解答:
解:配方可得f(x)=
-
=
-
,
构造点P(x,0),A(-
,
),B(
,
),
函数f(x)的值域表示|PA|-|PB|的取值范围.
由于三角形的两边之差小于第三边,
∴||PA|-|PB||<|AB|=1,
故函数f(x)的值域为:(-1,1).
故答案为:(-1,1)
| x2+x+1 |
| x2-x+1 |
=
(x+
|
(x-
|
构造点P(x,0),A(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
函数f(x)的值域表示|PA|-|PB|的取值范围.
由于三角形的两边之差小于第三边,
∴||PA|-|PB||<|AB|=1,
故函数f(x)的值域为:(-1,1).
故答案为:(-1,1)
点评:本题考查函数的值域,考虑几何意义是解决问题的关键,属中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列函数为奇函数的是( )
A、y=x
| ||
| B、y=lgx2 | ||
| C、1og2x | ||
D、y=2x-
|
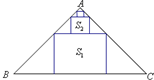 在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则
在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则| lim |
| n→∞ |
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2的值为( )
| A、-4 | B、-10 | C、-8 | D、-6 |
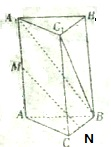 如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.
如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.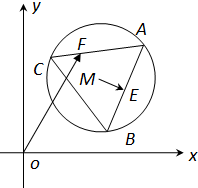 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,同时点F在边AC上运动时,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,同时点F在边AC上运动时,