题目内容
设函数f(x)=sin(ωx-
)-2cos2
x+1(ω>0),直线y=
与函数y=f(x)图象相邻两交点的距离为π.(Ⅰ)求ω的值;
(Ⅱ)求函数f(
-x)的单调递增区间.
| π |
| 6 |
| ω |
| 2 |
| 3 |
(Ⅱ)求函数f(
| π |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,复合三角函数的单调性
专题:三角函数的求值,三角函数的图像与性质
分析:(I)先化简解析式得f(x)=
sin(ωx-
),根据已知可求函数f(x)的最小正周期T=π,从而可求ω的值;
(Ⅱ)由(I)先求得解析式f(
-x)=-
sin(2x-
),从而可求其单调递增区间.
| 3 |
| π |
| 3 |
(Ⅱ)由(I)先求得解析式f(
| π |
| 3 |
| 3 |
| π |
| 3 |
解答:
解:(I)f(x)=sinωxcos
-cosωxsin
-cosωx,即f(x)=
sin(ωx-
)
∵直线y=
与函数y=f(x)图象相邻两交点的距离为π.
∴函数f(x)的最小正周期T=π,即
=π,
可得ω=2…(6分)
(Ⅱ)由(I)知f(x)=
sin(2x-
),
∴f(
-x)=
sin(
-2x)=-
sin(2x-
),
由2kπ+
≤2x-
≤2kπ+
,k∈Z可解得kπ+
≤x≤kπ+
,k∈Z
∴函数f(
-x)的单调递增区间[kπ+
,kπ+
],k∈Z…(12分)
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 3 |
∵直线y=
| 3 |
∴函数f(x)的最小正周期T=π,即
| 2π |
| ω |
可得ω=2…(6分)
(Ⅱ)由(I)知f(x)=
| 3 |
| π |
| 3 |
∴f(
| π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
∴函数f(
| π |
| 3 |
| 5π |
| 12 |
| 11π |
| 12 |
点评:本题主要考察了由y=Asin(ωx+φ)的部分图象确定其解析式,复合三角函数的单调性,综合性较强,属于中档题.

练习册系列答案
相关题目
设函数f(x)=ax(a>0且a≠1),f(2)=9,则f(
)=( )
| 1 |
| 2 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
阅读如图的程序框图,运行相应的程序,则输出S的值为( )


| A、8 | B、18 | C、26 | D、80 |
下列函数为奇函数的是( )
A、y=x
| ||
| B、y=lgx2 | ||
| C、1og2x | ||
D、y=2x-
|

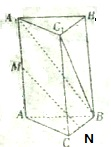 如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.
如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.