题目内容
在2点至3点之间的某一时刻,分针与时针分别在钟面上“2”字的两侧,而且与“2”字的距离相等,这一时刻是( )
A、2时6
| ||
B、2时7
| ||
C、2时8
| ||
D、2时9
|
考点:函数的零点
专题:计算题,应用题,函数的性质及应用
分析:由题意可判断分针在“2”字的上侧,时针在“2”字的下侧,设这一时刻为2时x分,则从2点到此时刻分针转过的角度大小为(6x)°,时针转过的角度大小为(
x)°,从而可列出方程60-6x=
x,从而解得.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:显然分针在“2”字的上侧,时针在“2”字的下侧,
且分针速度是6°/分钟,时针速度是(
)°/分钟.
设这一时刻为2时x分,
则从2点到此时刻分针转过的角度大小为(6x)°,时针转过的角度大小为(
x)°.
从而可列出方程60-6x=
x,
解得x=9
.
所以这一时刻应是2时9
分.
故选D.
且分针速度是6°/分钟,时针速度是(
| 1 |
| 2 |
设这一时刻为2时x分,
则从2点到此时刻分针转过的角度大小为(6x)°,时针转过的角度大小为(
| 1 |
| 2 |
从而可列出方程60-6x=
| 1 |
| 2 |
解得x=9
| 3 |
| 13 |
所以这一时刻应是2时9
| 3 |
| 13 |
故选D.
点评:本题考查了函数在实际问题中的应用,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
某产品的广告费用x与销售额y的统计数据如表:
根据表中可得线性回归方程
=
x+
中的
为9.4,据此模型预报广告费用为7万元时销售额为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 26 | 39 | 49 | 54 |
| y |
| b |
| a |
| b |
| A、73.6万元 |
| B、73.8万元 |
| C、74.9万元 |
| D、75.1万元 |
设函数f(x)=ax(a>0且a≠1),f(2)=9,则f(
)=( )
| 1 |
| 2 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
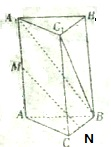 如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.
如图所示,三棱柱A1B1C1-ABC的底面是边长为1的正三角形,侧棱A1A⊥底面ABC且A1A=2,M、N分别为AA1、BC的中点.