题目内容
 已知抛物线C的顶点在原点,焦点在y轴上,抛物线上点M(x,4)(x>0)到准线的距离是5.
已知抛物线C的顶点在原点,焦点在y轴上,抛物线上点M(x,4)(x>0)到准线的距离是5.(Ⅰ)求抛物线C的方程;
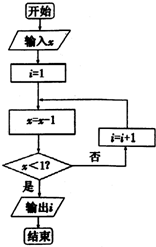
(Ⅱ)执行如图所示程序框图,若输入的x的值为M点的横坐标,请根据输出的i的值,求圆锥曲线C:
| x2 |
| i-3 |
| y2 |
| 8-i |
考点:程序框图,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程,算法和程序框图
分析:(Ⅰ)由题意,故可设抛物线方程为x2=2py(p>0),抛物线的准线方程为:y=-
,则有
+4=5,即解得p=2,可求抛物线C的方程.
(Ⅱ)由点M(x,4)(x>0)在抛物线x2=4y上,解得x=4,输入x=4,执行如图所示程序框图可得i=4,可得圆锥曲线C的方程为:x2+
=1,故可求e.
| p |
| 2 |
| p |
| 2 |
(Ⅱ)由点M(x,4)(x>0)在抛物线x2=4y上,解得x=4,输入x=4,执行如图所示程序框图可得i=4,可得圆锥曲线C的方程为:x2+
| y2 |
| 4 |
解答:
解:(Ⅰ)∵抛物线上点M(x,4),
∴抛物线的焦点在y轴的正半轴,故可设抛物线方程为x2=2py(p>0)…1分
∴抛物线的准线方程为:y=-
…3分
又∵点M(x,4)(x>0)到准线的距离是5…5分
∴
+4=5,即p=2
所以,抛物线C的方程为x2=4y…6分
(Ⅱ)∵点M(x,4)(x>0)在抛物线x2=4y上
∴x=4
∴输入x=4,执行如图所示程序框图可得:i=4…9分
∴可得圆锥曲线C的方程为:x2+
=1,是焦点在y轴上的椭圆
∴a=2,b=1
∴c=
=
∴e=
=
,所以椭圆的离心率为
…12分
∴抛物线的焦点在y轴的正半轴,故可设抛物线方程为x2=2py(p>0)…1分
∴抛物线的准线方程为:y=-
| p |
| 2 |
又∵点M(x,4)(x>0)到准线的距离是5…5分
∴
| p |
| 2 |
所以,抛物线C的方程为x2=4y…6分
(Ⅱ)∵点M(x,4)(x>0)在抛物线x2=4y上
∴x=4
∴输入x=4,执行如图所示程序框图可得:i=4…9分
∴可得圆锥曲线C的方程为:x2+
| y2 |
| 4 |
∴a=2,b=1
∴c=
| a2-b2 |
| 3 |
∴e=
| c |
| a |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了程序框图和算法,椭圆的简单性质,综合性较强,属于中档题.

练习册系列答案
相关题目
下列函数中,与函数y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=
| ||
| C、y=logaax | ||
D、y=(
|
已知命题P:关于x的函数f(x)=2x2+ax+2,在区间[1,+∞)上是增函数,命题q:关于x的方程x2-ax+a=0有实数根.若p∨q为真命题,p∧q为假命题,则实数a的取值范围是( )
| A、(-4,4)∪(4,+∞) |
| B、(-∞,-4) |
| C、(-∞,-4)∪(0,4) |
| D、[-4,+∞) |
设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1=
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
| 1 |
| 2 |
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
若执行如图所示的程序框图,输出S的值为( )


| A、2log23 |
| B、log27 |
| C、3 |
| D、2 |
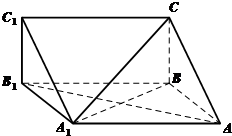 如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.
如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.