题目内容
已知命题P：关于x的函数f（x）=2x2+ax+2，在区间[1，+∞）上是增函数，命题q：关于x的方程x2-ax+a=0有实数根．若p∨q为真命题，p∧q为假命题，则实数a的取值范围是（ ）
| A、（-4，4）∪（4，+∞） |
| B、（-∞，-4） |
| C、（-∞，-4）∪（0，4） |
| D、[-4，+∞） |
考点：复合命题的真假
专题：简易逻辑
分析：命题P1：关于x的函数f（x）=2x2+ax+2=2(x+
)2=2-
，在区间[1，+∞）上是增函数，可得-
≤1；命题q：关于x的方程x2-ax+a=0有实数根，则△≥0．由p∨q为真命题，p∧q为假命题，可得p与q必然一真一假，即可得出．
| a |
| 4 |
| a2 |
| 8 |
| a |
| 4 |
解答：
解：命题P1：关于x的函数f（x）=2x2+ax+2=2(x+
)2=2-
，在区间[1，+∞）上是增函数，∴-
≤1，解得a≥-4；
命题q：关于x的方程x2-ax+a=0有实数根，则△=a2-4a≥0．解得a≥4或a≤0．
若p∨q为真命题，p∧q为假命题，
则p与q必然一真一假，
∴
或
，
解得0＜a＜4或a＜-4．
则实数a的取值范围是0＜a＜4或a＜-4．
故选：C．
| a |
| 4 |
| a2 |
| 8 |
| a |
| 4 |
命题q：关于x的方程x2-ax+a=0有实数根，则△=a2-4a≥0．解得a≥4或a≤0．
若p∨q为真命题，p∧q为假命题，
则p与q必然一真一假，
∴
|
|
解得0＜a＜4或a＜-4．
则实数a的取值范围是0＜a＜4或a＜-4．
故选：C．
点评：本题考查了二次函数的单调性、一元二次方程有实数根与判别式的关系、简易逻辑的判定，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设集合 A={1，2，3，4}，B={3，5}，C={2}，则 A∩（B∪C）=（ ）
| A、{2} | B、{2，3} |
| C、{3} | D、{1，3} |
在直角坐标系中，点A，B，C的坐标分别为(0，1)，(
，0)，(0，-2)，O为坐标原点，动点P满足|
|=1，则|
+
+
|的最小值是（ ）
| 2 |
| CP |
| OA |
| OB |
| OP |
A、4-2
| ||
B、
| ||
C、
| ||
D、
|
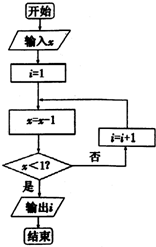
阅读如图的程序框图，若输入m=2，n=3，则输出a=（ ）
| A、6 | B、4 | C、3 | D、2 |
已知抛物线C的顶点在原点，焦点在y轴上，抛物线上点M（x，4）（x＞0）到准线的距离是5．