题目内容
设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1=
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
| 1 |
| 2 |
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
考点:抽象函数及其应用
专题:函数的性质及应用,等差数列与等比数列
分析:根据f(x)•f(y)=f(x+y),令x=n,y=1,可得数列{an}是以
为首项,以
为等比的等比数列,进而可以求得Sn,进而Sn的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵对任意x,y∈R,都有f(x)•f(y)=f(x+y),
∴令x=n,y=1,得f(n)•f(1)=f(n+1),
即
=
=f(1)=
,
∴数列{an}是以
为首项,以
为等比的等比数列,
∴an=f(n)=(
)n,
∴Sn=
=1-(
)n∈[
,1).
故选C.
∴令x=n,y=1,得f(n)•f(1)=f(n+1),
即
| an+1 |
| an |
| f(n+1) |
| f(n) |
| 1 |
| 2 |
∴数列{an}是以
| 1 |
| 2 |
| 1 |
| 2 |
∴an=f(n)=(
| 1 |
| 2 |
∴Sn=
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题主要考查了等比数列的求和问题,解题的关键是根据对任意x,y∈R,都有f(x)•f(y)=f(x+y)得到数列{an}是等比数列,属中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
在直角坐标系中,点A,B,C的坐标分别为(0,1),(
,0),(0,-2),O为坐标原点,动点P满足|
|=1,则|
+
+
|的最小值是( )
| 2 |
| CP |
| OA |
| OB |
| OP |
A、4-2
| ||
B、
| ||
C、
| ||
D、
|
一排有6个座位,三个同学随机就坐,任何两人不相邻的坐法种数为( )
| A、120 | B、36 | C、24 | D、72 |
当x<0时,函数f(x)=(2a-1)x的值恒大于1,则实数a的取值范围是( )
A、(
| ||
| B、(1,2) | ||
| C、(1,+∞) | ||
| D、(-∞,1) |
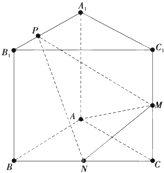 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,AB⊥AC,M、N分别是CC1、BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,AB⊥AC,M、N分别是CC1、BC的中点,点P在线段A1B1上,且 已知抛物线C的顶点在原点,焦点在y轴上,抛物线上点M(x,4)(x>0)到准线的距离是5.
已知抛物线C的顶点在原点,焦点在y轴上,抛物线上点M(x,4)(x>0)到准线的距离是5.