题目内容
18.若x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$,则z=x+2y的最大值与最小值的差为( )| A. | 3 | B. | 4 | C. | 7 | D. | 10 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数求出最小值和最大值,作差得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$作出可行域如图,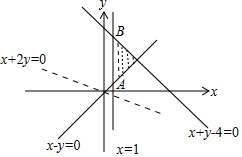
联立$\left\{\begin{array}{l}{x=1}\\{x-y=0}\end{array}\right.$,解得A(1,1);
联立$\left\{\begin{array}{l}{x=1}\\{x+y-4=0}\end{array}\right.$,解得B(1,3).
作出直线x+2y=0,由图可知,当直线x+2y=0分别平移至A和B时,目标函数z=x+2y取得最小值和最大值.
最小值为3,最大值为7.
∴z=x+2y的最大值与最小值的差为7-3=4.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
10.一个几何体的三视图如图所示(其中主视图的弧线为四分之一圆周),则该几何体的体积为( )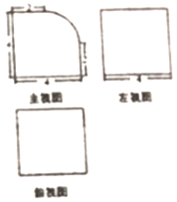

| A. | 64-4π | B. | 64+6π | C. | 48+4π | D. | 64-6π |
7.已知M是抛物线x2=16y上任意一点,A(0,4),B(-1,1),则|MA|+|MB|的最小值为( )
| A. | $\sqrt{10}$ | B. | 3 | C. | 8 | D. | 5 |
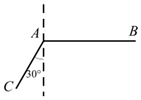 如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.
如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$. 已知在四棱锥C-ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点.
已知在四棱锥C-ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点.