题目内容

3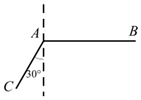．如图，当甲船位于A处时获悉，在其正东方向相距10海里的B处有个艘渔船遇险等待营救，甲船立即前往营救，同时把消息告知在甲船的南偏西30°，相距6海里的C处的乙船，乙船立即朝北偏东（θ+30°）的方向沿直线前往B处营救，则sinθ的值为$\frac{5\sqrt{3}}{14}$．

分析 连结BC，先用余弦定理计算BC，再利用正弦定理计算sinC即可．

解答 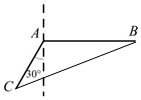解：连结BC，由已知得AC=6，AB=10，∠BAC=120°，
由余弦定理得BC2=AB2+AC2-2•AB•AC•cos120°=100+36-2•10•6•（-$\frac{1}{2}$）=196，
∴BC=14，
由正弦定理得$\frac{AB}{sinC}=\frac{BC}{sin∠BAC}$，即$\frac{10}{sinC}=\frac{14}{\frac{\sqrt{3}}{2}}$，解得sinC=$\frac{5\sqrt{3}}{14}$，
∴sinθ=$\frac{5\sqrt{3}}{14}$．
故答案为：$\frac{5\sqrt{3}}{14}$．

点评 本题考查了解三角形的实际应用，正余弦定理在解三角形中的应用，属于中档题．

练习册系列答案
相关题目
13．已知椭圆$P：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的右焦点为F（1，0），且经过点$（{\frac{2}{3}，\frac{{2\sqrt{6}}}{3}}）$
（1）求椭圆P的方程；
（2）已知正方形ABCD的顶点A，C在椭圆P上，顶点B，D在直线7x-7y+1=0上，求该正方形ABCD的面积．
14．已知数列{an}和{bn}满足：${a_{n+k}}-{（{-1}）^k}•{a_n}={b_n}（n∈{N^*}）$．
（1）若$k=1，{a_1}=1，{b_n}={2^n}$，求数列{an}的通项公式；
（2）若k=4，bn=8，a1=4，a2=6，a3=8，a4=10．
①求证：数列{an}为等差数列；
②记数列{an}的前n项和为Sn，求满足${（{{S_n}+1}）^2}-\frac{3}{2}{a_n}+33={k^2}$的所有正整数k和n的值．
11．已知△ABC的内角A，B，C对边分别为a，b，c，若满足$\frac{2c-b}{a}$=$\frac{cosB}{cosA}$，且$a=2\sqrt{5}$，则△ABC面积的最大值5$\sqrt{3}$．
18．若x，y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$，则z=x+2y的最大值与最小值的差为（　　）
A．3B．4C．7D．10
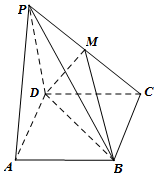8．如图，四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥平面ABCD，且△PAD是边长为2的等边三角形，$PC=\sqrt{13}$，点M是PC的中点．
（I）求证：PA∥平面MBD；
（II）求四面体P-BDM的体积．
15．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点P（$\sqrt{3}$，1）且离心率为$\frac{\sqrt{6}}{3}$，F为椭圆的右焦点，过F的直线交椭圆C于M，N两点，定点A（-4，0）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若△AMN面积为3$\sqrt{3}$，求直线MN的方程．
12．已知函数f（x）=sin（$\frac{x}{4}$-$\frac{π}{3}$），若存在实数x1，x2使得对任意实数x，都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值是（　　）
A．8πB．4πC．2πD．π
12．化简：
（1）sin（-α）cos（-α-π）tan（2π+α）；
（2）$\frac{sin（180°+α）cos（-α）}{tan（-α）}$；
（3）$\frac{cos（α+π）sin（-α）}{cos（-3π-α）sin（-α-4π）}$；
（4）sin2（-α）+tan（2π+α）cos2（π+α）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网