题目内容
已知函数f(x)=loga(x+b)的图象经过点(-3,0),和(0,-2),则a+b的值是 .
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据对数函数的性质代入可解得.
解答:
解:∵函数f(x)=loga(x+b)的图象经过点(-3,0),和(0,-2),
∴loga(-3+b)=0,loga(0+b)=-2,
∴
,
解得b=4,a=
,
∴a+b=
故答案为:
.
∴loga(-3+b)=0,loga(0+b)=-2,
∴
|
解得b=4,a=
| 1 |
| 2 |
∴a+b=
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题主要考查了对数函数的性质,属于基础题.

练习册系列答案
相关题目
在(x-y)10的展开式中,系数最小的项是( )
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
“lgx,lgy,lgz成等差数列”是“y2=xz”成立的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
直线x+
y=0被圆x2+y2-4y=0所截得的弦长为( )
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
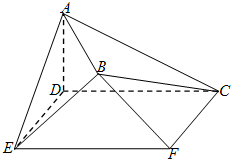 如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=
如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=