题目内容
“lgx，lgy，lgz成等差数列”是“y2=xz”成立的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据对数的运算lgx，lgy，lgz成等差数列，得出y2=xz，再根据充分必要条件的定义可判断．
解答：
解：∵∴2lgy=lgx+lgz
即∴若“lgx，lgy，lgz成等差数列”则“y2=xz”成立
反之，y=0．x=0，则对数没有意义，
∴根据充分必要条件的定义可判断：
“lgx，lgy，lgz成等差数列”是“y2=xz”成立的充分不必要条件
故选：A
即∴若“lgx，lgy，lgz成等差数列”则“y2=xz”成立
反之，y=0．x=0，则对数没有意义，
∴根据充分必要条件的定义可判断：
“lgx，lgy，lgz成等差数列”是“y2=xz”成立的充分不必要条件
故选：A
点评：本题考察了对数的概念，运算，充分必要条件的定义，属于中档题．
练习册系列答案
相关题目
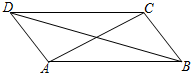如图，平行四边形ABCD中，向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
sin(2π-α)cos(
| ||||
tan(α-3π)sin(
|
| A、-cosα | B、cosα |
| C、sinα | D、-sinα |
若条件p：|x+1|＞2，条件q：x＞a且￢p是￢q的充分不必要条件，则a取值范围是（ ）
| A、a≥1 | B、a≤1 |
| C、a≥-3 | D、a≤-3 |
已知函数f（x）=loga（x+1），a＞1，对于定义域内的x1，x2有0＜x1＜x2＜1，给出下列结论：
①（x2-x1）[f（x2）-f（x1）]＜0；
②x2f（x1）＜x1f（x2）；
③f（x2）-f（x1）＞x1-x2；
④
＜f（
）．
其中正确结论的序号是（ ）
①（x2-x1）[f（x2）-f（x1）]＜0；
②x2f（x1）＜x1f（x2）；
③f（x2）-f（x1）＞x1-x2；
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
其中正确结论的序号是（ ）
| A、①② | B、①③ | C、②④ | D、③④ |
在长为5cm的线段AB上任取一点C，以AC，BC为邻边作一矩形，则矩形面积不小于4cm2的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
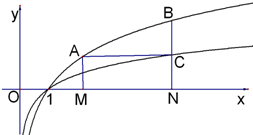如图，过函数f（x）=logcx（c＞1）的图象上的两点A，B作x轴的垂线，垂足分别为M（a，0），N（b，0）（b＞a＞1），线段BN与函数g（x）=logmx，（m＞c＞1）的图象交于点C，且AC与x轴平行．已知锐角α的终边上一点P（sin40°，1+cos40°），则α等于（ ）
| A、10° | B、20° |
| C、70° | D、80° |