题目内容

设
a
=（-
3
，1），
b
=（cosα，-sinα）．
（1）若
a
⊥
b
，求
sinα+cosα
sinα-cosα
的值；
（2）若|
a
-
b
|=
7
，求
a
与
b
夹角θ的大小．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由
a
⊥
b
，可得
a
•
b
=-
3
cosα-sinα=0，sinα=-
3
cosα≠0．代入
sinα+cosα
sinα-cosα
即可得出．
（2）由已知可得|
a
|=2，|
b
|=1，|
a
-
b
|=
7
，数量积运算性质可得
a
2+
b
2-2
a
•
b
=
7
，化为
a
•
b
=-1．
利用cosθ=
a
•
b
|
a
||
b
|
即可得出．
解答： 解：（1）∵
a
⊥
b
，∴
a
•
b
=-
3
cosα-sinα=0，
∴sinα=-
3
cosα≠0．
sinα+cosα
sinα-cosα
=
-
3
cosα+cosα
-
3
cosα-cosα
=
3
-1
3
+1
=
4-2
3
2
=2-
3
；
（2）∵|
a
|=2，|
b
|=1，|
a
-
b
|=
7
，
∴
a
2+
b
2-2
a
•
b
=
7
，
∴4+1-2
a
•
b
=7，
∴
a
•
b
=-1．
∴cosθ=
a
•
b
|
a
||
b
|
=
-1
2
，
∴θ=
2π
3
．
点评：本题考查了数量积运算性质、向量夹角公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图，如图所示，则该截面的面积是
 
．
已知
a
=（cos（α+β），sin（α+β）），
b
=（cosβ，sinβ），且|
.
a
-
b
|=1，求
（1）cosα的值；
（2）在[0，π]内，求∠α的度数．
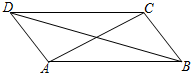如图，平行四边形ABCD中，向量
AC
=(1，
3
)，
BD
=（-2，0），则
AC
与
AB
的夹角为（　　）
A、
π
2
B、
π
3
C、
π
4
D、
π
6
如图，在边长为2的正三角形ABC中，点P满足
CP
=2
PB
，则
AP
•
CB
=
 
．
设关于x的不等式x2-2x-（a2-2a）＜0的解集为A，若2∈A，则实数a的取值范围为（　　）
A、（0，2）
B、（-∞，0）
C、（2，+∞）
D、（-∞，0）∪（2，+∞）
在直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，记ρ为极径，θ为极角，设曲线ρsin（θ-
π
4
）=2
2
关于直线sinθ=cosθ对称的曲线为C，则C的极坐标方程是
 
．
已知函数f（x）=loga（x+b）的图象经过点（-3，0），和（0，-2），则a+b的值是
 
．
在长为5cm的线段AB上任取一点C，以AC，BC为邻边作一矩形，则矩形面积不小于4cm2的概率为（　　）
A、
1
5
B、
2
5
C、
3
5
D、
4
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网