题目内容
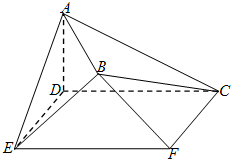 如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=
如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=| 2 |
(Ⅰ)求平面ABE与平面ABF所成的锐二面角的余弦值;
(Ⅱ)已知点M,N分别在线段DF,BC上,且DM=λDF,CN=μCB.若MN⊥平面BCF,求λ,μ的值.
考点:用空间向量求平面间的夹角,二面角的平面角及求法
专题:空间位置关系与距离
分析:(Ⅰ)分别以DE,DC,DA为x,y,z轴,建立空间直角坐标系,利用向量法能求出平面ABE与平面ABF所成的锐二面角的余弦值.
(Ⅱ)由
=λ
,得M(λ,2λ,0),由
=μ
,得N(μ,2-μ,μ).由此利用向量法能求出λ=μ=
.
(Ⅱ)由
| DM |
| DF |
| CN |
| CB |
| 1 |
| 2 |
解答:
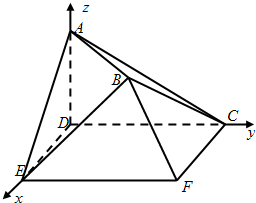 (本小题满分14分)
(本小题满分14分)
解:(Ⅰ)如图,分别以DE,DC,DA为x,y,z轴,
建立空间直角坐标系.
则有A(0,0,1),D(0,0,0),E(1,0,0),F(1,2,0),C(0,2,0).
又平面BEF⊥底面CDEF,则点B的横坐标为1,
由BE=BF=
,EF=2,
得点B的纵坐标和竖坐标都为1,即B(1,1,1).
设平面ABE的法向量为
=(x,y,z),
又
=(-1,0,1),
=(0,1,1),
得
,取z=1,得
=(1,-1,1).
设平面ABF的法向量为
=(x,y,z),
又
=(1,1,0),
=(0,-1,1),
得
,取y=-1,得
=(1,-1,-1).
由cos<
,
>=
=
,
得平面ABE与平面ABF所成的锐二面角的余弦值为
.….(7分)
(Ⅱ)由
=λ
,得M(λ,2λ,0),
同理由
=μ
,得N(μ,2-μ,μ).
则
=(λ-μ,2λ+μ-2,-μ),
由
,
得λ=μ=
.…..(14分)
 (本小题满分14分)
(本小题满分14分)解:(Ⅰ)如图,分别以DE,DC,DA为x,y,z轴,
建立空间直角坐标系.
则有A(0,0,1),D(0,0,0),E(1,0,0),F(1,2,0),C(0,2,0).
又平面BEF⊥底面CDEF,则点B的横坐标为1,
由BE=BF=
| 2 |
得点B的纵坐标和竖坐标都为1,即B(1,1,1).
设平面ABE的法向量为
| n |
又
| EA |
| EB |
得
|
| n |
设平面ABF的法向量为
| m |
又
| AB |
| FB |
得
|
| m |
由cos<
| n |
| m |
| ||||
|
|
| 1 |
| 3 |
得平面ABE与平面ABF所成的锐二面角的余弦值为
| 1 |
| 3 |
(Ⅱ)由
| DM |
| DF |
同理由
| CN |
| CB |
则
| NM |
由
|
得λ=μ=
| 1 |
| 2 |
点评:本题考查平面ABE与平面ABF所成的锐二面角的余弦值的求法,考查λ,μ的值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
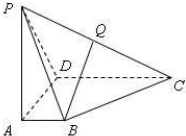 如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=| 1 |
| 2 |
(1)求证:PD⊥AB;
(2)在侧棱PC上是否存在一点Q,使BQ∥平面PAD?证明你的结论.
已知F是椭圆
+
=1(a>b>0)的右焦点,过点F作斜率为2的直线l使它与圆x2+y2=b2相切,则椭圆离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
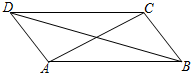 如图,平行四边形ABCD中,向量
如图,平行四边形ABCD中,向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
