题目内容
在（x-y）10的展开式中，系数最小的项是（ ）
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
考点：二项式定理的应用
专题：计算题,二项式定理
分析：由二项展开式可得出系数最小的项系数一定为负，再结合组合数的性质即可判断出系数最小的项．
解答：
解：展开式共有11项，奇数项为正，偶数项为负，且第6项的二项式系数最大，
则展开式中系数最小的项第6项．
故选C．
则展开式中系数最小的项第6项．
故选C．
点评：本题考查二项式系数的性质，考查学生的分析能力，正确运用二项式系数的性质是关键．
练习册系列答案
阅读快车系列答案
相关题目
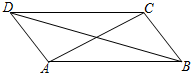如图，平行四边形ABCD中，向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
设关于x的不等式x2-2x-（a2-2a）＜0的解集为A，若2∈A，则实数a的取值范围为（ ）
| A、（0，2） |
| B、（-∞，0） |
| C、（2，+∞） |
| D、（-∞，0）∪（2，+∞） |
sin(2π-α)cos(
| ||||
tan(α-3π)sin(
|
| A、-cosα | B、cosα |
| C、sinα | D、-sinα |
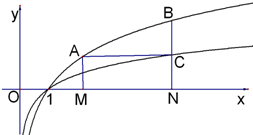如图，过函数f（x）=logcx（c＞1）的图象上的两点A，B作x轴的垂线，垂足分别为M（a，0），N（b，0）（b＞a＞1），线段BN与函数g（x）=logmx，（m＞c＞1）的图象交于点C，且AC与x轴平行．