题目内容
直线x+
y=0被圆x2+y2-4y=0所截得的弦长为( )
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:首先根据已知题意分析圆心与半径.通过直线与圆相交构造一个直角三角形.直角边分别为半弦长,弦心距.斜边为半径.按照勾股定理求出半弦长,然后就能求出弦长.
解答:
解:根据题意,圆为x2+y2-4y=0
故其圆心为(0,2),半径为:2
圆心到直线的距离为:d=
=
由题意,圆的半径,圆心到直线的距离,以及圆的弦长的一半构成直角三角形
故由勾股定理可得:l=2
=2
故选:B.
故其圆心为(0,2),半径为:2
圆心到直线的距离为:d=
|2
| ||
|
| 3 |
由题意,圆的半径,圆心到直线的距离,以及圆的弦长的一半构成直角三角形
故由勾股定理可得:l=2
| 4-3 |
故选:B.
点评:本题考查直线与圆的方程的应用,首先根据圆分析出圆的要素,然后根据直线与圆相交时构造的直角三角形按照勾股定理求出结果.属于基础题

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
在长为5cm的线段AB上任取一点C,以AC,BC为邻边作一矩形,则矩形面积不小于4cm2的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
A、5
| ||
B、20
| ||
C、15
| ||
D、10
|
“x=kπ+
(k∈Z)“是“tanx=1”成立的( )
| π |
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知锐角α的终边上一点P(sin40°,1+cos40°),则α等于( )
| A、10° | B、20° |
| C、70° | D、80° |
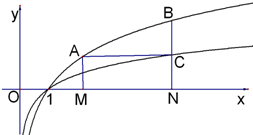 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.