题目内容
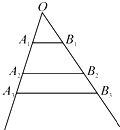如图，互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上，所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．设OAn=an，若a1=1，a2=2，则a9=考点：平行线等分线段定理
专题：计算题,立体几何
分析：本题可以根据所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．然后利用所有的三角形都相似，面积比等于相似比的平方，得出一系列的等式，然后利用累乘法求得通项，进一步求得结果．
解答：
解：依题意：互不相同的点A1，A2，…，An，…和B1，B2，…，Bn，…分别在角O的两条边上．
∵所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．
∴利用所有的三角形都相似，面积比等于相似比的平方，
若a1=1，a2=2，则令S△OA1B1=m（m＞0），
∴S梯形A1B1A2B2=3m，
∴当n≥2时，
=
=
，
故an2=
an-12，
利用以累乘可得：an2=（3n-2）a12，
由于a1=1，
∴an=
，
∴a9=5．
故答案为：5．
∵所有AnBn相互平行，且所有梯形AnBnBn+1An+1的面积均相等．
∴利用所有的三角形都相似，面积比等于相似比的平方，
若a1=1，a2=2，则令S△OA1B1=m（m＞0），
∴S梯形A1B1A2B2=3m，
∴当n≥2时，
| an |
| an-1 |
| OAn |
| OAn-1 |
|
故an2=
| 3n-2 |
| 3n-5 |
利用以累乘可得：an2=（3n-2）a12，
由于a1=1，
∴an=
| 3n-2 |
∴a9=5．
故答案为：5．
点评：本题应用知识较多：平行线分线段成比例定理，相似三角形面积比等于相似比的平方，数列通项中的累乘法，
练习册系列答案
阅读快车系列答案
相关题目
设函数f（x）=x2─2，用二分法求f（x）=0的一个近似解时，第1步确定了一个区间为（1，
），到第3步时，求得的近似解所在的区间应该是（ ）
| 3 |
| 2 |
A、（1，
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
曲线y=
与直线x=1，x=e2及x轴所围成的图形的面积是（ ）
| 1 |
| x |
| A、e2 |
| B、e2-1 |
| C、e |
| D、2 |
已知函数f（x）=ax2-|x|+2a-1（a为实常数）．