题目内容
已知抛物线C:y2=2px(p>0)的焦点为F,点Q是抛物线C上一点且Q的纵坐标为4,点Q到焦点F的距离为5.
(Ⅰ)求抛物线方程;
(Ⅱ)已知p<8,过点M(5,-2)任作一条直线与抛物线C相交于点A,B,试问在抛物线C上是否存在点E,使得EA⊥EB总成立?若存在,求出点E的坐标,若不存在,请说明理由.
(Ⅰ)求抛物线方程;
(Ⅱ)已知p<8,过点M(5,-2)任作一条直线与抛物线C相交于点A,B,试问在抛物线C上是否存在点E,使得EA⊥EB总成立?若存在,求出点E的坐标,若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意有Q(
,4),则有|QF|=
+
=5,由此能求出抛物线方程.
(Ⅱ)由已知得y2=4x.假设在抛物线C上存在点E,使得EA⊥EB总成立.设A(x1,y1),B(x2,y2),E(x0,y0),则y1y2+y0(y1+y2)+y02+16=0.设直线方程为x=m(y+2)+5,代入y2=4x中,有y2-4my-8m-20=0,由此能求出在抛物线C上存在点E(1,2),使得
•
=0总成立.
| 8 |
| p |
| 8 |
| p |
| p |
| 2 |
(Ⅱ)由已知得y2=4x.假设在抛物线C上存在点E,使得EA⊥EB总成立.设A(x1,y1),B(x2,y2),E(x0,y0),则y1y2+y0(y1+y2)+y02+16=0.设直线方程为x=m(y+2)+5,代入y2=4x中,有y2-4my-8m-20=0,由此能求出在抛物线C上存在点E(1,2),使得
| EA |
| EB |
解答:
解:(Ⅰ)由题意有Q(
,4),则有|QF|=
+
=5,
解得p=2或p=8,
所以,抛物线方程为y2=4x或y2=16x.…(5分)
(Ⅱ)∵p<8,∴y2=4x.
假设在抛物线C上存在点E,使得EA⊥EB总成立.
设A(x1,y1),B(x2,y2),E(x0,y0),
则有(x1-x0)(x2-x0)+(y1-y0)(y2-y0)=0,
即
+(y1-y0)(y2-y0)=0,
又(y1-y0)(y2-y0)≠0,
得(y1+y0)(y2+y0)+16=0,
即y1y2+y0(y1+y2)+y02+16=0,…①…(9分)
设直线方程为x=m(y+2)+5,代入y2=4x中,
有y2-4my-8m-20=0,从而y1+y2=4m,且y1y2=-8m-20,
代入①中得:(4y0-8)m+y02-4=0对于m∈R恒成立,
故4y0-8=0,且y02-4=0,解得y0=2,得E(1,2).…(14分)
若直线过点(1,2),结论显然成立
所以,在抛物线C上存在点E(1,2),使得
•
=0总成立.…(15分)
| 8 |
| p |
| 8 |
| p |
| p |
| 2 |
解得p=2或p=8,
所以,抛物线方程为y2=4x或y2=16x.…(5分)
(Ⅱ)∵p<8,∴y2=4x.
假设在抛物线C上存在点E,使得EA⊥EB总成立.
设A(x1,y1),B(x2,y2),E(x0,y0),
则有(x1-x0)(x2-x0)+(y1-y0)(y2-y0)=0,
即
| (y12-y02)(y22-y02) |
| 16 |
又(y1-y0)(y2-y0)≠0,
得(y1+y0)(y2+y0)+16=0,
即y1y2+y0(y1+y2)+y02+16=0,…①…(9分)
设直线方程为x=m(y+2)+5,代入y2=4x中,
有y2-4my-8m-20=0,从而y1+y2=4m,且y1y2=-8m-20,
代入①中得:(4y0-8)m+y02-4=0对于m∈R恒成立,
故4y0-8=0,且y02-4=0,解得y0=2,得E(1,2).…(14分)
若直线过点(1,2),结论显然成立
所以,在抛物线C上存在点E(1,2),使得
| EA |
| EB |
点评:本题考查抛物线方程的求法,考查在抛物线C上存在点E使得
•
=0总成立的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.
| EA |
| EB |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数f(x)=ex(x≤0)的反函数为y=f-1(x),则函数y=f-1(2x-1)的定义域为( )
| A、(0,1] | ||
| B、(-1,1] | ||
C、(-∞,
| ||
D、(
|
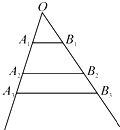 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=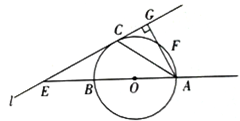 已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
已知:直线AB过圆心O,交⊙O于A、B,直线AF交⊙O于A、F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.