题目内容
设函数f(x)=x2─2,用二分法求f(x)=0的一个近似解时,第1步确定了一个区间为(1,
),到第3步时,求得的近似解所在的区间应该是( )
| 3 |
| 2 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:把x=1,
,
,
,
代入函数解析式,分析函数值的符号是否异号即可.
| 3 |
| 2 |
| 5 |
| 4 |
| 11 |
| 8 |
| 23 |
| 16 |
解答:
解:令f(x)=x2-2,
则f(1)=-1<0,则f(
)>0,
f(
)=-
<0,
所以到第二步求得的近似解所在的区间应该是(
,
);
f(
)=-
<0,
由f(
)f(
)<0知到第3步时,求得的近似解所在的区间应该是在(
,
).
故选:C.
则f(1)=-1<0,则f(
| 3 |
| 2 |
f(
| 5 |
| 4 |
| 7 |
| 16 |
所以到第二步求得的近似解所在的区间应该是(
| 5 |
| 4 |
| 3 |
| 2 |
f(
| 11 |
| 8 |
| 7 |
| 64 |
由f(
| 11 |
| 8 |
| 3 |
| 2 |
| 11 |
| 8 |
| 3 |
| 2 |
故选:C.
点评:此题考查二分法求方程的近似解,以及方程的根与函数的零点之间的关系,体现了转化的思想,同时也考查了学生分析解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点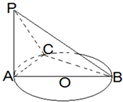 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )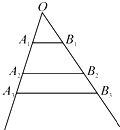 如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=
如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an,若a1=1,a2=2,则a9=